Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 22/09/2021 M'écrire Brèves de Maths

INDEX Polygones Géométrie	Polygones inscrits
	Polygone	Polygone inscrit	Carré-Carré

Polygones inscrits n-gone inscrit dans un m-gone Comment dessiner un polygone à n côtés dans un polygone à m côtés ? Pas de méthode générale, surtout si les polygones ne sont pas réguliers. Le cas le plus classique: un carré dans un polygone régulier. L'outil GeoGebra sera d'un grand secours.
	Sommaire de cette page >>> Le	Débutants Nombres Glossaire Nombres

Approche – Carré dans un octogone régulier		haut
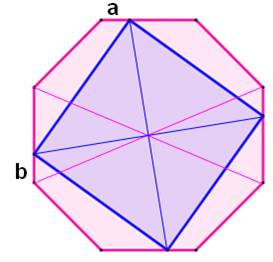
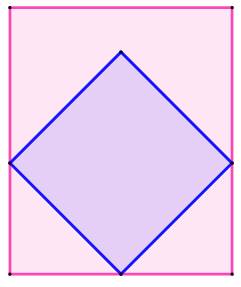
Figure Un carré bleu inscrit dans un octogone rouge. Propriétés Pour des raisons de symétries, les diagonales du carré et de l'octogone se coupent au même point, le centre géométrique (de gravité) de chacun des polygones. Il existe une infinité de tels carrés inscrits. Les longueurs a et b sont égales.

Approche – Carré dans un hexagone quelconque		haut
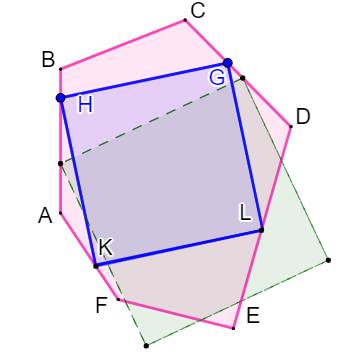
Figure Un carré bleu inscrit dans un hexagone quelconque (convexe) rouge. Construction avec GeoGebra Mettre les points H et G sur objet AB et CD, deux côtés du polygone. Dessiner le polygone régulier avec quatre côtés à partir de GH. Ce carré est quelconque pour le moment (carré pointillé vert). Déplacer les point G et H pour positionner les points K et L sur l'hexagone (carré bleu). La solution est souvent unique. Résultat En reproduisant le polygone que vous étudiez, vous obtiendrez une solution approchée à votre problème. Ne pas hésitez à zoomer la figure pour positionner K été L.

Recherche du carré et comparaison des aires

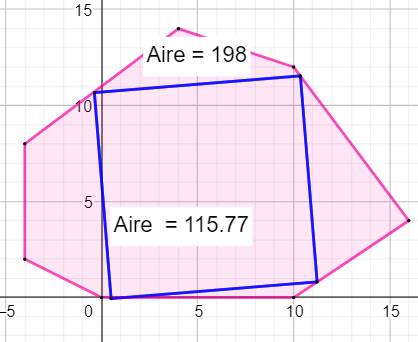
Étude de cas	haut
Étude de cas

Carré dans quadrilatère quelconque

haut

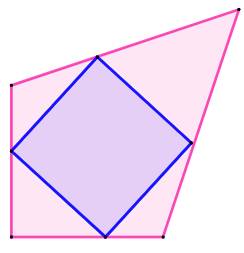
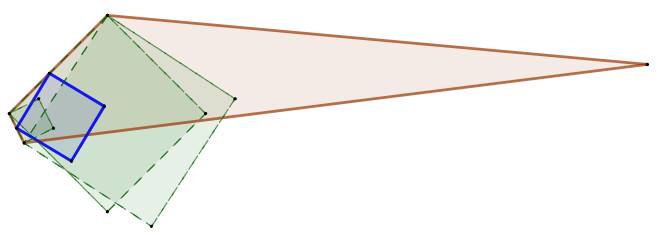
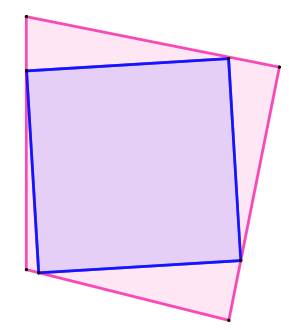
Cette figure montre qu'il n'est pas toujours possible d'inscrire un carré avec chacun des sommets sur un côté dans un quadrilatère quelconque. En bleu une tentative. En vert, la latitude de débattement du carré bleu lorque les des deux sommets nagiquenet sue les deux côtés de gauche. Mon affirmation est contraire à celle de ce chercheur américain qui affirme le contraire: En revanche, s'il s'agit d'inscrire le carré dans le quadrilatère une solution comme celles-ci est toujours possible:

Polygones réguliers		haut
Théorème	Deux polygones réguliers avec n et m côtés. Le m-gone peut être inscrit dans le n-gone, si et seulement si l'une de ces conditions est satisfaite: a) m = 3 b) m = 4 c) m > 4 si m divise n d) m > 5 est pair et n est impair ou un multiple de m/2 Dans les cas c et d les polygones sont concentriques. Dans le cas d, les polygones partagent un axe de symétrie.
Dans le pentagone et l'hexagone Autour du triangle équilatéral

Haut de page

Retour	Polygones réguliers
Suite
Voir
Sites
Cette page	http://villemin.gerard.free.fr/GeomLAV/Polygone/Inscrits.htm