|
|||||||||||||||||||||||||||||
![]()
|
Étude 67 – Somme 67 Sur cette page, étape 4, nous allons compter les
additions de quatre termes valant de 1 à 100 et produisant une somme de 67.
(Cette valeur étant prise comme exemple). |
Voir Nombre
67
|
|
||
|
|
1 + 66 = 67 2 + 65 = 67 … 33 + 34 = 67 33 sommes égales à 67 sur 5 050 |
|
|
|
||
|
|
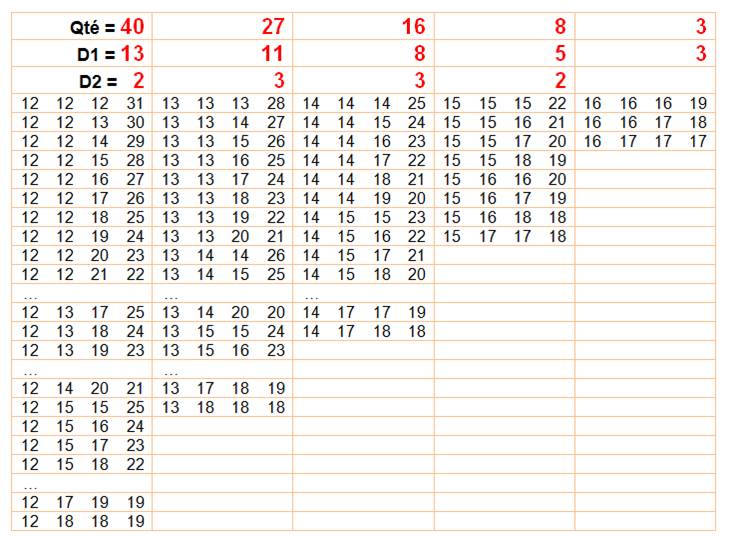
1 + 1 + 65 = 67 1 + 2 + 64 = 67 … 1 + 33 + 33 = 67 2 + 2 + 63 = 67 2 + 3 + 62 = 67 … 2 + 32 + 33 = 67 3 + 3 + 61 = 67 3 + 4 + 60 = 67 … 3 + 32 + 32 = 67 … / … 20 + 20 + 27 = 67 20 + 21 + 26 = 67 20 + 22 + 25 = 67 20 + 23 + 24 = 67 21 + 21 + 25 = 67 21 + 22 + 24 = 67 21 + 23 + 23 = 67 22 + 22 + 23 = 67 374 sommes égales à 67 sur 171 700 |
|
|
|
|
|
2 178 sommes égales à 67 sur 4 421 275 |
|
|
Le dénombrement
des additions distinctes de n termes valant de 1 à 100 avec une somme égale à
100 sont au nombre de: n = 1 n = 2 n = 3 n = 4 Total: 2 586 Ce décompte, à ma
connaissance, n'est pas des plus simples ! |
|
|
|
|
|
|
![]()
|
Retour |
|
|
Voir |
|
|
Cette page |
![]()