|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
PARTITIONS en sommes d'entiers Décomposition d'un nombre en sommes de nombres. Base des carrés
magiques. Vers la conjecture
de Goldbach. |
|
|
||||
|
Partition des nombres
entiers Le nombre n est décomposé en sommes.
Toutes les sommes possibles sans tenir compte de l'ordre des termes. Alors 2
+ 3 et 3 + 2 comptent pour une seule partition. Chaque somme est une partition de n;
sa décomposition en parts. Les termes de la somme sont appelées
les sommants ou parts de la partition. La quantité de partitions de n est
notée: P(n) |
Les 7 partitions du
nombre 5
P(5) = 7 Les nombres sommants sont rangés par ordre
croissant en descendant les lignes |
|||
|
Notations (3 types) Exemple avec le nombre 5. |
|
|||
|
Composition des
nombres entiers Toutes les partitions déclinées en
tenant compte des permutations des termes. On parle aussi de décompositions
ou de partitions induites. Ainsi, la deuxième partition du nombre 5, le
nombre 2 unique peut prendre l'une des quatre places dans la somme, soit 4
compositions. La quantité de compositions de N est égale à la
puissance N – 1 de 2. >>> |
Les
16 compositions du nombre 5
C(5) = 16 = 25 – 1 |
|||
|
Les questions que l'on
se pose
Partition des
ensembles
|
N = a + b + c + … Exemples 10 = 1 + 2 + 3 +
4 10² = 13
+ 23 + 33 + 43 5² = 3² + 4² 3² = 1 + 3 + 5 33 = 7 + 9 + 11 Voir Pépites |
|||
|
|
|||||||
|
Liste de toutes les
partitions des chiffres, rangées par catégories:
|
P(n) = quantité totale de partitions
du nombre n, y compris le nombre lui-même. |
||||||
|
n |
P(n) |
Biparttion |
Tripartition |
4-partition |
n-partition |
||
|
1 |
|
|
|
|
|||
|
2 |
1, 1 |
|
|
|
|||
|
3 |
1, 2 |
1, 1,
1 |
|
|
|||
|
5 |
1, 3 |
1, 1,
2 |
1, 1,
1, 1 |
|
|||
|
7 |
1, 4 |
1, 1,
3 |
1, 1,
1, 2 |
1, 1,
1, 1, 1 |
|||
|
|
|
2, 3 |
1, 2,
2 |
|
|
||
|
11 |
1, 5 |
1, 1,
4 |
1, 1,
1, 3 |
1, 1,
1, 1, 2 |
|||
|
|
|
2, 4 |
1, 2, 3 |
1, 1,
2, 2 |
1, 1,
1, 1, 1, 1 |
||
|
|
|
3, 3 |
2, 2, 2 |
|
|
||
|
15 |
1, 6 |
1, 1,
5 |
1, 1,
1, 4 |
1, 1,
1, 1, 3 |
|||
|
|
|
2, 5 |
1, 2,
4 |
1, 1,
2, 3 |
1, 1,
1, 2, 2 |
||
|
|
|
3, 4 |
1, 3,
3 |
1, 2,
2, 2 |
1, 1,
1, 1, 1, 2 |
||
|
|
|
|
2, 2,
3 |
|
1, 1,
1, 1, 1, 1, 1 |
||
|
22 |
1, 7 |
1, 1,
6 |
1, 1,
1, 5 |
1, 1,
1, 1, 4 |
|||
|
|
|
2, 6 |
1, 2,
5 |
1, 1,
2, 4 |
1, 1,
1, 2, 3 |
||
|
|
|
3, 5 |
1, 3,
4 |
1, 1,
3, 3 |
1, 1,
2, 2, 2 |
||
|
|
|
4, 4 |
2, 2,
4 |
1, 2,
2, 3 |
1, 1,
1, 1, 1, 3 |
||
|
|
|
|
2, 3,
3 |
2, 2, 2, 2 |
1, 1,
1, 1, 2, 2 |
||
|
|
|
|
|
|
1, 1,
1, 1, 1, 1, 2 |
||
|
|
|
|
|
|
1, 1,
1, 1, 1, 1, 1, 1 |
||
|
30 |
1, 8 |
1, 1,
7 |
1, 1,
1, 6 |
1, 1,
1, 1, 5 |
|||
|
|
|
2, 7 |
1, 2,
6 |
1, 1,
2, 5 |
1, 1,
1, 2, 4 |
||
|
|
|
3, 6 |
1, 3,
5 |
1, 1,
3, 4 |
1, 1,
1, 3, 3 |
||
|
|
|
4, 5 |
2, 2,
5 |
1, 2,
2, 4 |
1, 2,
2, 2, 2 |
||
|
|
|
|
1, 4,
4 |
1, 2,
3, 3 |
1, 1,
2, 2, 3 |
||
|
|
|
|
2, 3,
4 |
2, 2,
2, 3 |
1, 1,
1, 1, 2, 3 |
||
|
|
|
|
3, 3, 3 |
|
1, 1,
1, 1, 1, 4 |
||
|
|
|
|
|
|
1, 1,
1, 2, 2, 2 |
||
|
|
|
|
|
|
1, 1,
1, 1, 1, 1, 3 |
||
|
|
|
|
|
|
1, 1,
1, 1, 1, 2, 2 |
||
|
|
|
|
|
|
1, 1,
1, 1, 1, 1, 1, 2 |
||
|
|
|
|
|
|
1, 1,
1, 1, 1, 1, 1, 1, 1 |
||
Compléments
en
Partitions des nombres de
1 à 10
|
|
|||
|
On peut compter les partitions ou se
référer à une liste établie (Tableau). Voir
l'encyclopédie des suites de nombres: A000041
– a(n) = number of partitions of n (the partition numbers). |
|
||
|
Avoir recours à un logiciel de
calcul mathématqiue: Exemple
avec Maple et son logiciel
spécialisé: combinat
(combinatoire). L'instruction numbpart fournit immédiatement la quantité de
partitions. L'instruction
seq
demande de calculer la même chose pour n de 1 à 30. |
|
||
|
Faire une division de polynôme. |
|
||
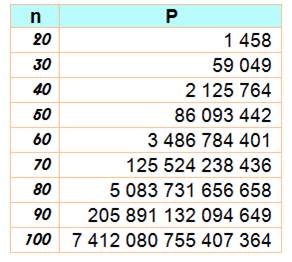
Suite en Quantité
de partitions
|
|
|||||||||||||||||||||||||||
|
Plus grand P(n)
premier P(n)
est premier pour n = 6, alors P(n) = 11, par exemple. Le
plus grand n, avec P(n) premier, connu en
2017 comporte plus de 16 000 chiffres. |
Exemples
DifTri =
Tripartition avec des nombres tous différents |
||||||||||||||||||||||||||
Voir Partitions du nombre 36 pour
construire une étoile magique (avec tableur et avec logiciel)
|
|
|||
|
Diagramme de Ferrers
d'une partition Exemple d'une partition de 13: chaque ligne est
totalisée et on énonce ces totaux de chaque ligne: 5 + 3 + 3 + 2 = 13. |
|
||
|
Tableaux de Young
d'une partition Semblable avec des carrés au lieu de point. Ils sont utilisés en combinatoire. |
|
||
|
Toutes les partitions
d'un nombre Le
diagramme de Ferrers est un moyen astucieux de représenter toutes les
partitions d'un nombre. Avec la partition du nombre 5, on joue à réaliser
des pentaminos:
assemblages divers de cinq carrés. Sur
chaque pentamino, on compte la quantité de carrés horizontaux: 3 + 1 + 1; 2 +
1 + 1, 2 + 1 + 1 + 1 et 1 + 1 + 1 + 1 + 1 sur la partie du haut. Le
diagramme est symétrique par rapport à la diagonale. Deux partitions
symétriques sont dites conjuguée ou duales. |
|
||
|
Partitions avec
restrictions Partition de n = 10 avec r = 3 comme terme
maximum; soit trois colonnes seulement Remarquez la somme indiquée en horizontal:
10 = 5 + 3 + 2, ce qui normal, on n'a
pas perdu de carrés en route! Le diagramme tourné d'un quart de tour est le conjugué de
l'initial. De
manière aussi logique, on peut imaginer une rotation de 45°, avec, ici selon
les diagonales, la partition: 1 + 2 +
3 + 3 + 1. Ça marche car la quantité de carrés sur la figure est bien
évidemment constante. |
|
||
|
|
|||
|
Reprenons
le diagramme de Ferrers du nombre 5 et observons les partitions de
différentes couleurs. Le
diagramme suffit à montrer l'égalité des quantités de partitions partielles
suivantes:
Propriétés La quantité de partitions faite de k sommants est
égale à celle faite avec les nombres k PS (5, k) = PN (5, k) |
|
||
|
Il n'y a
qu'une seule partition avec un seul sommant (ici, le 5) et qu'une seule
partition avec le nombre 1. |
Il y a
deux partitions avec deux sommants (ici, 1+4 et 2+3) et deux partitions avec
le nombre 2 (comprendre impliquant le nombre 2, mais pas plus). |
||
Suite en Dénombrement des partitions partielles
Voir Partitions distinctes et
théorème des nombres pentagonaux
![]()
|
|
|||
|
Quelle est la partition d'un nombre qui engendre le
plus grand produit de ses termes? Quelle est la partition la plus généreuse? |
Exemple pour 10:
|
||
|
On peut monter que les termes au-delà de 4
n'introduisent pas de bénéfice. En fait 3 est l'optimum, puis complétez par
des 2. Ex: 10 = 5 +
5 => 25; 10 = 3 + 2 + 5 => 30; le 5 remplacé par 3 + 2 est plus
généreux. |
Règle de constitution
de la partition la plus généreuse:
|
||
|
Exemples de partitions
généreuses: |
|
||
|
Quelques valeurs du
produit généreux |
|
||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Addition/PttIntro.htm |
![]()