NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 19/01/2017 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Jeux et énigmes
Débutants Général	SPORTS				Glossaire Général
INDEX Loisirs	Football	Golf	Équipes	Tournois
		Ronde au golf
		Sommaire de cette page >>> 16 golfeurs par quatre sur cinq jours - Solution Étude de ce cas >>> Cas de 4 joueurs en équipes de 2 >>> Cas de 6 joueurs en équipes de 3 >>> Cas de 7 joueurs en équipes de 2 >>> Cas de 16 joueurs en équipes de 4 >>> Bilan pour 16 en équipe de 4 >>> Table de composition des équipes

Ronde sociale

16 joueurs en équipe de 4

Voici une association de 16 joueurs de golf qui s'apprête à mettre en place un tournoi. Chaque partie oppose quatre joueurs. Combien de parties sont nécessaires pour que chaque joueur puisse rencontrer chacun des membres de l'association? La réponse est cinq.

Trouver la solution n'est pas simple.

Sur cette page on donne la solution et on explore la recherche de solution. Impasse!

En fait, de nombreux mathématiciens ont étudié ce type d'organisation dite ronde sociale. La solution n'existe pas toujours. Voir historique

16 golfeurs par quatre sur cinq jours

Seize golfeurs décident de jouer par groupe de quatre. Ils disposent de cinq jours à raison d'un tournoi par jour. Comment organiser les parties de sorte qu'un golfeur ne rencentre jamais un autre deux fois ou plus? Graphe de la solution La solution est présentée sous forme d'un graphe astucieux en étoile. Chaque sommet (noir) est un golfeur. Un trait réunis quatre points (golfeurs) et la couleur représentent les jours de tournoi. Graphe mis en tableau Les seize joueurs jouent tous un jour donné (chaque ligne) et, en fin de tournoi, ils auront joué quatre fois. De plus, chaque joueur aura joué une fois avec chacun des participants (voir colonne 1 pour le joueur A, par exemple).

Anglais: Can 16 golfers each play in foursomes for 5 days? / Resolvable Steiner quadruple system (RSQS)

Voir cas de 15 en groupe de 3 et 20 en groupes de 4.

La référence donne d'autres exemples de situations avec solutions.

Étude montrant une méthode de recherche de solution

Cette recherche avait été faite avant que je connaisse la solution

Intérêt d'archive uniquement

Cas de 4 joueurs en équipes de 2
Nous dénombrons six équipes: Le joueur 4 joue avec 3 puis avec 2 et enfin avec 1 3 équipes. Le joueur 3 a déjà joué avec 4, il lui reste à jouer avec 2 puis avec 1 2 équipes. Le jouer 2 a déjà joué avec 4 et avec 3, il lui reste à jouer avec 1 1 équipe. Total: 3 + 2 + 1 = 6 équipes. Utile pour la suite, nous allons former la table des partenaires. Elle montre qui a joué avec qui. Sa complétion indique que chacun a joué avec tous ses partenaires. On élimine les diagonales, le joueur ne joue pas avec lui-même La table est symétrique. Si 4 joue avec 4, 3 joue avec 4! Nous éliminons également une moitié de la table. Nous remplissons la table à partir de la table des équipes. Par exemple(en jaune) 3 joue avec 4, alors la case 34 est mise à 1 Vous vérifierez vous-mêmes que les six cases de la table sont parfaitement remplies. Ce qui montre que nous disposons de toutes les équipes nécessaires répondant aux exigences du tournoi.

Bilan

Avec 4 joueurs en équipes de 2, le tournoi sera réalisé avec 6 équipes (ou 6 parties). Notons que 6 c'est le nombre de combinaisons de 2 parmi 4:

Est-ce toujours comme cela? Hélas, non! Ça se complique.

Cas de 6 joueurs en équipes de 3
Avec six joueurs en équipe de 3, les choses se compliquent. Il est impossible de faire concourir tout le monde en ne se rencontrant qu'une seule fois. Il faut introduire des parties où certains rejouent ensemble. Après avoir formé quatre équipes de 3 joueurs (la première étant 6, 5 ,4; puis 6, 3, 2; etc.), nous sommes dans l'impossibilité d'aller plus loin sans doublonner. L'analyse de la table des partenaires (2 joue avec 1; puis 3 joue avec 1; etc.) montre que (en jaune) 1-6, 2-5 et 3-4 ne se sont pas encore rencontrés Nous constatons que trois jeux supplémentaires sont nécessaires. En rouge, d'autres joueurs pris au hasard parmi les autres pour compléter l'équipe de 3. Bilan Sept équipes (ou sept parties) sont nécessaires pour faire le tournoi de six joueurs en équipes de 3.	Tables des équipes et des partenaires Équipes supplémentaires

Cas de 7 joueurs en équipes de 3
Nous avons 7 équipes impeccables! Par contre, impossible de compter via les combinaisons, ce qui donnerait: Ici, intervient une réduction importante du fait des doublons. Voyez le début du tableau: etc. Seules les configurations en jaune sont retenues; les autres disparaissent.	Tables des équipes et des partenaires

Bilan

Avec 4 joueurs par 2 ou avec 7 joueurs par 3, il est possible de former des équipes optimales (sans doublons). Il y a respectivement 6 et 7 équipes par tournoi.

Avec 6 joueurs par 3, impossible d'éviter les doublons et il y faut 7 parties pour réaliser le tournoi complet. Et ce type de cas est le plus fréquent.

Cas de 16 joueurs en équipes de 4
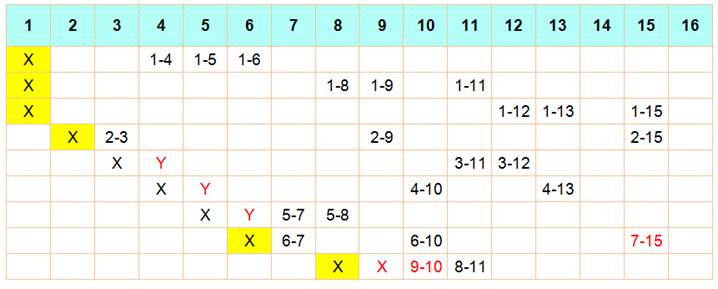
Dans ce cas, il est possible de former 16 équipes sans redondances. Mais, hélas, il manque beaucoup de rencontres entre joueurs comme le montre le tableau des partenaires. Manquent: 1-4, 1-5, 1-6, 1-8, 1-9, 1-11, 1-12, 1-13, 1-15 2-3, 2-9, 2-15 3-11, 3-12, 4-10, 4-13 5-7, 5-8 6-7, 6-10 7-15 8-11 9-10 Nous allons examiner les cas manquants tout en essayant d'optimiser la quantité des équipes. Par exemple, on fera se rencontrer le 1 avec tous les autres en seulement trois équipes (les trois premières lignes du tableau ci-dessous). Pour le 2, une seule équipe suffit (ligne 4 du tableau). Ces lignes sont marquées en jaune pour indiquer qu'elles sont complètes. Par contre les suivantes sont incomplètes. Le tableau plus bas montre les déplacements (en rouge) qui permettent une réduction du nombre d'équipes. Bilan 16 + 9 = 25 équipes >>>	Table des équipes et des partenaires Table des partenaires
Examen des cas complémentaires Optimisation Soit 2 lignes en moins. Pour trois lignes non complètes (pas en jaune), il faut choisir un joueur quelconque (Y) pour compléter m'équipe à 4.

Bilan des équipes pour 16 joueurs par équipes de 4

Pour les équipes de 1 à 16 (en jaune), les joueurs rencontrent toujours des nouveaux.

Pour les équipes de 17 à 25, certains joueurs se retrouvent.

Pour les équipes 21, 22 et 23, il est possible de choisir n'importe quel partenaire parmi les autres joueurs pour ceux notés en rouge.

Table de composition d'équipes

En jaune les cas de composition d'équipe sans doublons. Pour les autres, on indique, par exemple pour 9 joueurs par équipe de 3: 8 + 6 (12) qui veut dire: 8 équipes composées sans doublon (cette information est sûre). 6 équipes avec doublons. Cette quantité est un maximum. (12) indique que 12 cas de partenariats ne sont pas satisfaits ce qui impose les 6 équipes complémentaires. Si une optimisation est possible, elle ne peut pas descendre en dessous de 12 / 3 (joueurs) = 4 équipes. Bilan: la quantité d'équipes est au plus de 8 + 6 = 14, mais pas moins de 8 + 4 = 12.

Suite	Voir haut de page Golf Tournois Jeux et énigmes – Index
DicoNombre	Nombre 18
Site	Social Golfer Problem – Math Game – Ed Pegg Jr – 2007 – Quelques exemples de configuration de social golfers Warwick's Results Page for the Social Golfer Problem – Warwick Harvey – Table des situations avec solution de social golfers (Cliquer sur le nombre dans le tableau pour accéder aux solutions)
Cette page	http://villemin.gerard.free.fr/aSport/Equipes.htm