|
||||||||||||||||||||||||||||
![]()
|
COMBINAISONS
– Introduction Sélection sans ordre et sans répétitions
|
|
|
|||
|
Il fait
chaud. je m'arrête chez le marchand de glace. Il a cinq
parfums par cornet (ou coupe) à deux boules. Combien de
possibilités de cornets avec à chaque fois deux parfums différents?
Pas la vanille, car vanille-chocolat c'est déjà fait et c'est la même
chose que chocolat-vanille.
Total: 4 + 3 + 2 + 1 = 10 choix de 2
parmi 5 Le
compte parait simple, en fait c'est un peu plus compliqué … |
|
||
|
Nous
cherchons toutes les possibilités d'un choix de 3 couleurs parmi 5. En listant
les possibilités, on trouve également 10 combinaisons. Pas facile à dénombrer
! Bilan: 10 choix de 2 parmi 5 Bizarre ! C'est la même quantité (10) pour 2
parmi 5 et 3 parmi 5. Le calcul n'est pas direct, il passe
par le calcul des arrangements:
choix de 3 parmi 5 dans l'ordre. Par exemple avec Jaune, Orange et
Vert, on a : JOR, JVO, OJV, OVJ, VJO et VOJ. Soit 6 fois trop de possibilités
par rapport à ce que l'on veut. Le calcul des combinaisons compte
alors les arrangements et divise le résultat par la quantité de possibilités
en trop. La formule sera expliquée plus bas. Pour
le moment contentons nous de l'astuce de calcul.
|
|
||
|
Truc pratique
pour compter vite les combinaisons de 2 parmi 5:
L'astuce
est générale avec p parmi n:
Notez
les nombreuses simplifications immédiates. |
Deux
parfums parmi cinq
Trois
parfums parmi cinq
Quatre
parfums parmi dix
Voir Autres valeurs
(triangle de Pascal) |
||
SVP, montrez-moi
un autre exemple pratique tout de suite >>>
Sinon, je continue
ci-dessous pour les explications théoriques.
![]()
|
|
||||||
|
L'ordre
n'a pas importance. Un élément
choisi, ne peut plus être re-choisi. C'est un tirage sans remise,
c'est-à-dire sans répétition. |
|
|||||
|
Exemple avec des
chiffres
|
||||||
|
|
||
|
Une telle
disposition s'appelle:
|
Voir explications de la Notation |
|
|
|
||||||||||||||||||||
|
Il existe
une relation simple entre les arrangements et les combinaisons
Pour bien
insister!
4 combinaisons et 4 x 6 arrangements de 3
parmi 4 |
||||||||||||||||||||
|
Ne
pas confondre deux cas typiques:
|
|
|
||
|
|
Voir Types de dispositions – Tableau complet |
|
|
|
||
|
Le nombre de combinaisons de p
éléments d'un ensemble à n éléments est le nombre défini par:
Pour 0 Il s'agit du coefficient du binôme. Voir son calcul
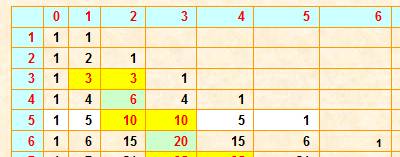
pratique et astuce. On retrouve toutes ces valeurs dans
le triangle
de Pascal.
Exemple: 3 parmi 6 = 20 Oups! Je n'y comprends rien avec
votre formule, vous n'avez pas plus simple! >>> Calculateur en ligne
|
||
|
|
||
|
Duels
télévisés:
avec 10 candidats aux élections, il faudrait 45 duels pour être équitable:
|
BRIDGE:
52 cartes, 13 par joueurs.
Soit environ 635 milliards de mains. |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
On veut
savoir quel est le numéro d'une combinaison parmi toutes les combinaisons. Exemple: (2, 3, 4) est la 7e
combinaison de 3 parmi 5. Dans ce
cas le rang est donné par ce calcul:
Voir Valeurs dans le Triangle de
Pascal |
Combinaisons
ordonnées de 3 parmi 5
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Soit une
combinaison de k parmi n et une des combinaisons (C1, C2,
… Ck) dans l'ordre croissant. Le rang de
cette combinaison est donné par la formule indiquée. |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Exemple pour (1, 2, 5) |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Exemple pour (2, 4, 5) |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Exemple avec 3 parmi 6 20 combinaisons
=> |
[1, 2, 3], [1, 2, 4], [1, 2, 5], [1, 2, 6], [1, 3,
4], [1, 3, 5], [1, 3, 6], [1, 4, 5], [1, 4, 6], [1, 5, 6], [2, 3, 4], [2, 3,
5], [2, 3, 6], [2, 4, 5], [2, 4, 6], [2, 5,
6], [3, 4, 5], [3, 4, 6], [3, 5, 6], [4, 5, 6] |
|
Exemple pour (2, 4, 6) en 15e
position |
|
Merci à Alban Gaudel pour
sa contribution
![]()
|
Suite |
|
|
Retour |
|
|
Voir |
|
|
|
|
|
Site |
|
|
Cette page |
![]()