|
|||||||||||||||||||||||||||||||
![]()
|
TOURNOIS en double Olympiades Comment organiser des
tournois opposant deux personnes (tennis, Commençons par des tournois
simples et voyons la célèbre énigme de
Lucas dit de la promenade des huit
demoiselles en rang par deux. |
Anglais: Round Robin
scheduling / Tournament organization / League schedules
|
|
||
|
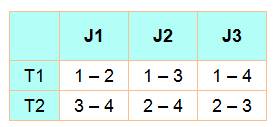
Les
joueurs (ou le équipes) sont nommées de 1 à 4. Le joueur
1 joue successivement contre les joueurs 2, 3 et 4. D'où les trois séances
(jours) de jeux sur le terrain 1 (T1). Pour
minimiser le temps, on fait jouer les autres équipes en parallèles sur le
second terrain (T2). La composition des équipes est immédiate: chaque jeu
fait intervenir les deux joueurs qui ne sont pas en train de jouer sur T1. |
Le jour 1 le match sur le terrain 1 oppose les joueurs 1 et 2; alors
que sur le terrain 2, se déroule le match entre les joueurs 3 et 4. Etc. |
|
|
|
|||
|
Une impasse! Avec 6
équipes, dénombrons la quantité d'épreuves (de matchs):
Soit 15 épreuves
en 5 jours sur 3 terrains. |
En reprenant le type de remplissage utilisé pour 4 équipes, nous
tombons sur une impossibilité. Pas facile de trouver la bonne configuration
en cherchant par tâtonnement. |
||
|
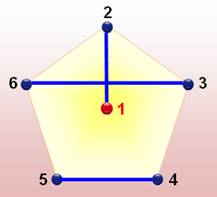
La
méthode consiste à créer un graphe
complet et à identifier les sous-graphes sans arêtes communes; avec chacun des
sommets ne recevant qu'une seule arête; un graphe
1-facteur (one-factor graph).
Avec ce
type de graphe à un facteur, chaque équipe est assurée de toutes se
rencontrer sans être mise à contribution deux fois. Avec le graphe central,
on a les équipes: 1-4, 2-6, et 3-5. Avec celui de gauche, on a: 1-2, 3-4 et
5-6. C'est une
bonne piste mais pas suffisante. L'astuce consiste à privilégier une des
équipes que nous ferons jouer contre toutes les autres et ensuite, nous
organiseront les autres matchs. Nous traduisons ce privilège sur le graphe en
introduisant un point central relié à tous les autres sommets |
|||
|
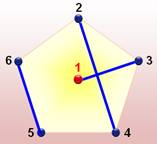
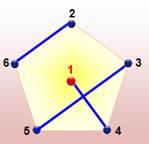
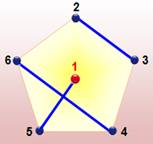
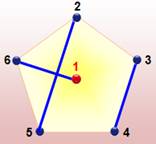
Tournoi de 6 équipes Graphe
avec le 1 au centre et les cinq autres équipes disposées aux sommets du pentagone.
Nous extrayons ce sous-graphe à un facteur (Illustration). Ce graphe
indique directement quelles sont les équipes à mobiliser pour le premier
tournoi: 1 – 2; 3 – 6; 4
– 5. Pour le
deuxième tournoi, relier 1 à 3 en faisant pivoter l'ensemble du sous-graphe
d'un cinquième de tour. La lecture des équipes à mettre en place est
immédiate. Ainsi de suite pour les cinq tournois successifs. |
|
||
|
Organisation des tournois sur les
cinq jours
|
|||
Bilan
|
La méthode Kirkman est systématique pour 2n joueurs. En cas de
nombre impair, un joueur sera oisif à chaque match. Son
point de départ peut-être tout autre sous-graphe à un facteur*. Nous allons prendre un nouvel exemple avec
la promenade des demoiselles étudiée par Édouard Lucas. *En
1980, Rosa et Wallis ont montré que si est grand (>7) c'est toujours vrai.
Sinon, il existe des cas avec faux départ. |
|
La promenade des
demoiselles (ou des jeunes-filles) par Édouard Lucas – 8
équipes |
|
||
|
Organisation de la promenade Huit
jeunes filles. Promenade
quotidienne en rang par deux. Comment
organiser la mise en rang de sorte qu'une fille se retrouve avec une fille
différente chaque jour? Combien de
jours avant d'avoir à recommencer le cycle? Généralisation Avec n
personnes, le cycle comporte n – 1 jours. Si n est
impair ajouter une personne fictive. La
résolution est du même type que celle décrite ci-dessous en portant n – 1 points sur le cercle. |
Tableau des promenades Le
premier jour, la promenade est faite comme suit: la fille 1 est avec la fille 8, puis
2 avec 7, puis 3 avec 6 et enfin 4 avec 5. Le
deuxième jour: 1 est avec 3, puis 2 avec 8, etc.
La ligne montre les partenaires de la fille 1
pour chaque jour. La ligne 2 montre les partenaires de la fille 2 de numéro supérieur à 2. Etc. Avec ce plan, après la septième journée, chaque fille aura côtoyé une
autre fille au cours des promenades. |
||
|
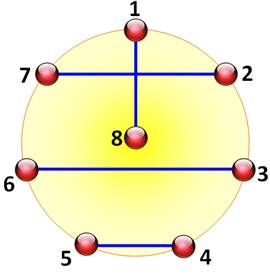
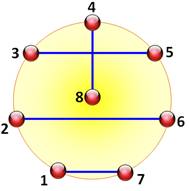
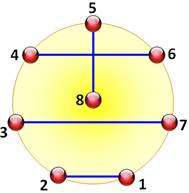
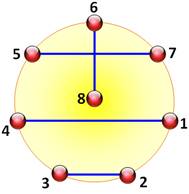
Construction du plan Claude
Berge propose un graphe qui permet de recomposer le tableau ci-dessus. Il est
issu d'une réflexion sur la coloration des graphes. La
première promenade est lue directement sur le graphe ci-contre: 1 avec 8; 2 avec 7; etc. La
deuxième se lit en ajoutant 1 à chaque sommet et en comptant modulo 7. Ainsi
2 est relié à 8, puis 3 à 1, puis 4 à 7, etc. (ci-dessous). |
|
||
|
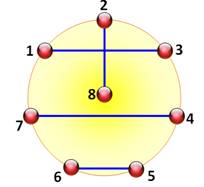
Les promenades suivantes
Note: La littérature montre un huit central, car les inventeurs de la
méthode souhaitaient que le centre soit particularisé est considéré comme
l'infini ( |
|||
|
|
||
|
Au
premier round, le jouer 1 est oisif tandis que trois matches se déroulent. On
applique la rotation classique et c'est le joueur 2 qui devient oisif. Etc.
|
|
|
|
De nos jours, la théorie des graphes
développée par Claude Berge
(1926-2002) porte réponse à certaines questions posées par Édouard Lucas. Le
problème de la "promenade des jeunes filles" revient à déterminer
la possibilité de couplage parfait d'un graphe, et celui de la
"ronde" consiste à rechercher le nombre de circuits hamiltoniens disjoints
d'un graphe bichromatique (deux couleurs). Anne-Marie Decaillot-Laulagnet La méthode indiquée ci-dessus a été mise au point en 1846 par Thomas P. Kirkman
(1806-1895). On ne sait pas de quand date son application à l'organisation de
tournoi. La littérature nomme aussi cette méthode: Steiner
method. Le problème des demoiselles a été remis à la mode par Lucas.
Cependant, c'est Kirkman le premier connu qui l'a
traité. Fifteen young ladies in a school (schoolgirls) walk
out three abreast for seven days in succession; it is required to arrange
them daily, so that no two shall walk twice abreast". Soit, 15 jeunes
filles en rang par trois sur sept jours. En 1850, Cayley et Kirkman donnent les
premières solutions écrites du problème des "schoolgirls".
Les problèmes de ce type sont appelés: Kirkman
Triple Systems; et leurs solutions: Steiner
Triple System. De tels problèmes ne sont pas toujours résolvables. En 1860, Pierce trouve les trois seules solutions à ce problème des 15
filles. D'autres suivront…avec à la clé des développements mathématiques
(théorie des graphes, Steiner triple system matrices d'Hadamard, greedy randomized adaptive search procedure (GRASP), notamment)
Voir Historique en
e-book |
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
|
|
|
Cette page |
![]()