|
|
Définition |
Le
but principal de la statistique est de déterminer les caractéristiques d'une
population donnée à partir de l'étude d'une partie de cette population,
appelée "échantillon". Statistique nom
féminin (allemand Statistik ;
du latin status, état) Définition
Larousse |
|
Étapes de l'analyse statistique |
Cinq étapes typiques de la pratique de la statistique: 1
Définition des unités statistiques, des variables, sur
lesquelles on va opérer: caractères comme la température, la taille, la
rémunération, les notes … 2
Recueil des données: mesures, enquêtes, sondages,
échantillonnage … 3
Présentation des données sous forme de tableaux, de
courbes, de graphiques … 4
Caractérisation de ces données par des paramètres.
statistiques caractéristiques: moyenne, médiane, mode, écart-type … 5
Extraction des conclusions: bilan narratif,
modélisation, expression de tendances, test des hypothèses, recherche de lien
entre caractères, de corrélations … Le
traitement des données s'appelle la statistique
descriptive (étapes 1 à 4); l'interprétation des données s'appelle l'inférence statistique ou statistique inférentielle (étape 5). |
![]()
|
Jargon! |
|
Voir Suite
![]()
|
Anglais |
For example, the
sample mean, the sample median and the sample variance are each a statistic. The sum of
observations in a sample is also a statistic, but this is not an estimator. |
|
En savoir plus |
|
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Vocabula/GlosS/Statisti.htm |
![]()
|
La
statistique est moins une science qu'un
art. Elle est la poésie des nombres.
Chacun y trouve ce qu'il y met. Albert Brie |
Voir Pensées & humour
![]()
Vocabulaire de base du domaine
de la statistique
|
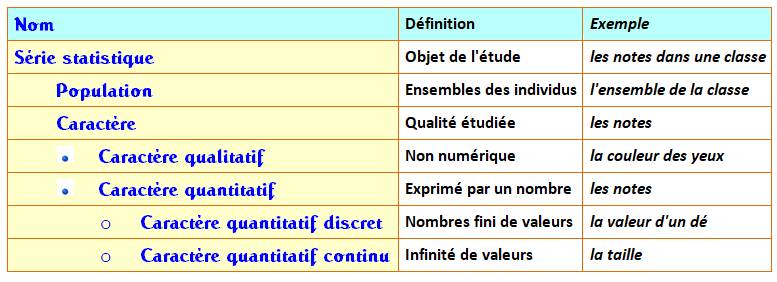
Caractère
Variable |
Âges dans une population, profondeurs dans une
mer donnée, notes dans une classe, rémunération des grands patrons, prix
d'achat d'un appartement dans une région … Caractère quantitatif: le prix d'un objet, la hauteur des arbres ou tout
autre critère d'étude en statistique auquel on peut donner une valeur; un
caractère quantitatif peut être: - soit discret
(ex: pointure des chaussures); - soit continu (ex:
tension mesurée aux bornes d'une pile). Caractère qualitatif: ce sont des noms et pas des nombres; ex: les
produits d'un magasin, le sexe d'une population, la couleur d'objets, la
nationalité …
|
![]()
|
Population Échantillon Effectif |
Exemple: les chaussures de la
famille
|
![]()
|
Série Étendue |
|
![]()
|
Fréquence |
C'est
une valeur comprise entre 0 et 1 qui peut aussi être exprimée sous la forme
d'un pourcentage. Exemple: La
fréquence de la pointure 40 est de 1 sur 7 soit 0,14 ou 14%.
|
![]()
|
Moyenne Médiane Mode |
Exemple: Trois
individus de 1,70m, 1,73m et 1,92 m, la moyenne est 1,78 m (somme des 3
valeurs divisée par 3).
|
![]()
|
Variance
Écart-type |
Ces
valeurs sont appelées paramètres de dispersion. Ils
permettent d'évaluer les écarts des valeurs des caractères par rapport à la
moyenne Plus
l'écart-type est grand plus la dispersion est grande. Note:
l'étendue est aussi un paramètre de dispersion. Quant à la moyenne, la
médiane, le mode et les quartiles,
ce sont des paramètres
de tendance. |
![]()
|
|
|
![]()
![]()
