|
||||||||||||||||||||||||||||||||||||||||
![]()
|
|
||
|
Général |
|
|
|
Arithmétique |
||
|
Géométrique |
||
|
Harmoniques |
|
|
|
Autres |
||
|
Propriétés |
||
![]()
|
Dessin humoristique avec jeu de mots anglais: - Oh, maman, ils me disent moyenne (average)! Les garçons ne peuvent pas être si
méchants (mean). - Non chérie, tu es la méchante / ou la moyenne (mean) Remarquez que le dessin est juste: m = (4+3+17) / 3 = 8 |
|
Voir
Pensées & humour
|
MOYENNES Introduction et
méthode de calcul. |
Voir Débutants
Voc
|
Moyenne
( Moyenne
pondérée B Espérance mathématique
(probabilité) Médiane (ne pas
confondre avec moyenne) Moyenne
généralisée |
|
Aver Me Arithmetic me Weighted Geometric me H Qu Generalized mean (power mean) Arithmetic-geometric me |
|
Soit une collection de n données { x1 , x2 , x3
… xi … xn } |
|
|
||
|
Deux
données C'est la demi-somme des deux données. |
|
|
|
Plusieurs
données Somme des données, divisée par la quantité de données. C'est la note moyenne
obtenue par un élève en classe (sans coefficient). |
Exemple 10, 12, 13 et 16 M = (11 +
12 + 13 + 16) / 4 = 13 |
|
|
Illustration
La moyenne arithmétique donne une valeur telle que la
somme des écarts (flèches bleues) est nulle. La somme de n fois la moyenne donne la somme des n
valeurs. Note
sur la moyenne et la progression: Les nombres { x1 , x2
, x3 … xi … xn
} sont dits en progression arithmétique, dans cet
ordre, si la distance qui les sépare est constante. Avec trois nombres,
si 2b = a + c alors b est la moyenne
arithmétique de a et c. Not
|
||
Voir Calculs et progression arithmétique
|
Parmi les nombres consécutifs
de 1 à n, on retire un nombre et on calcule la moyenne: 40,75. Quel est le
nombre retiré? |
|
|
||
|
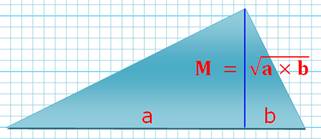
Deux données La moyenne géométrique de deux valeurs est la racine
carrée de leur produit Analogie C'est la propriété de la hauteur du triangle rectangle. |
|
|
|
Un rectangle de côtés a et b et un carré de côté c ont
même aire si c² = a.b (quadrature
du rectangle). Note: Dans le cas de
deux valeurs, on parle également de moyenne
proportionnelle. Plusieurs données La moyenne géométrique est égale à la racine nième du
produit des donnés.
Le produit de n fois la moyenne donne le produit des n
valeurs Exemple
{1000,
5000}
Avec le double de l'une et la moitié de l'autre, la
moyenne géométrique est identique, les deux facteurs (1/2 et 2) s'annihilant: {2000,
2500}
Cette moyenne s'applique lorsque les valeurs
proviennent de sources diverses, sachant que les sources sont fausses sans
doute de la même manière. La moyenne géométrique donne une valeur
"équitable" telle que le facteur d'erreur d'estimation des données
est atténué. Notation
mathématique
Qui se lit: la moyenne géométrique (x
barre) est la racine énième du produit (c'est la lettre Pi majuscule) de chacune
des valeurs xi pour i de 1 à n |
||
Voir Progression géométrique / Symboles / Triangle Sangaku
|
Moyenne pondérée entre
moyenne arithmétique et moyenne géométrique. Utile dans le calcul du volume
du tronc de prismes ou du tronc de cône.
|
Voir Volume du tronc de cône circulaire
/ Volume du tronc de cône
elliptique / Héron
|
|
||
|
Deux données La moyenne harmonique fait intervenir la somme des
inverses des nombres. À titre illustr |
|
|
|
Plusieurs données
C'est la moyenne arithmétique des inverses La moyenne harmonique intervient dans le calcul
La moyenne harmonique est toujours plus petite que les
deux autres, arithmétique et géométrique. |
||
Voir Série harmonique / Suite harmonique (Leibniz) / Harmonique / Spectre numérique / Les trois cercles
|
|
|
|
Suite Trois termes entretiennent entre eux une proportion
selon un excès donné et que l'excès du premier par rapport au deuxième est
celui du deuxième par rapport au troisième. 1, 2, 3 ou 2, 4, 6 Suite géométrique Le rapport des trois termes est tel que le premier
est au deuxième ce que le deuxième est au troisième.
1, 2, 4 ou 3, 6, 12 Suite h Trois termes tels que le premier terme dépasse le deuxième
d'une fraction de lui-même et le moyen dépasse le troisième de la même
fraction du troisième.
Exemples de suites
harmoniques de trois nombres: 3, 4, 6 ou 6, 8, 12
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()
Renvois de
liens
>>>
Comparaison
>>> Illustration géométrique
>>> Moyenne quadratique
>>> Moyenne arithmético – géométrique