|
|||||||||||||||||||||||||||||
![]()
|
FONCTION
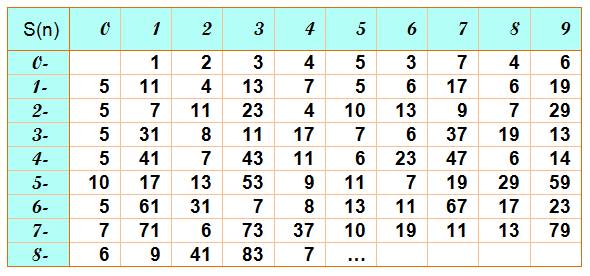
de SMARANDACHE Division des factorielles: quel est le plus petit entier qui ne divise
par la factorielle? |
Anglais: Smarandache
function
|
|
|
|
Exemple: avec 10, la
première valeur de factorielle divisible par 10 est 120 qui est 5! Alors S(10) = 5.
Rappel: le trait vertical se lit " divise". |
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
![]()