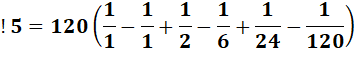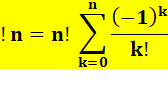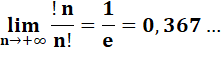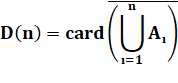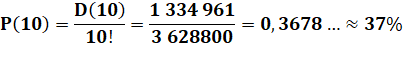|
|||||||||||||||||||||||||||||||||||||||
![]()
|
Dérangements et sous-factorielles En combinatoire, la notion de sous-factorielle permet de dénombrer les
dérangements: permutations
particulières telles qu'aucun des éléments initiaux ne se retrouve à sa place
initiale. En maths on dit: permutation
sans point fixe.
La quantité de dérangements
est notée D(n) ou a(n) ou encore !n (sous-factorielle de n). Cette valeur est
intimement liée à la constante e
= 2, 718 Exemple de dérangement: à la
sortie d'une réception, aucun des messieurs n'a son chapeau sur la tête. |
|
|
|
|
Exemple
Définition
pour n > 0, sinon !n = 1 – n (Ex: !0 = 1, !(-1) = 0; !(-2) =
-1). La sous-factorielle de n est égale
au produit de la factorielle de n par la somme pour toutes les valeurs prises
par k de 0 à n de (-1) à la puissance k divisée par factorielle k. Le (-1)k au numérateur
engendre la somme avec les signes alternés. Exemple de calcul de cette somme
Notez que: 0! = 1 et (-1)0
= 1. De sorte que les deux premiers termes de la parenthèse s'annulent. Table des premières valeurs
Curiosité 148
349 = !1 + !4 + !8 + !3 + !4 + !9 Voir DicoNombre
148 349 |
|
Voir Table jusqu'à !200
|
|
||
|
|
Première instruction a est la
sous-factorielle de n Deuxième instruction Calcul de la séquence des nombres sous-factorielles
de n pour n de 0 à 20). Le point-virgule indique que les valeurs doivent être
affichées. Résultat Toutes les
sous-factorielles des nombres de 0 à 20. Notez la valeur de !0 = 1. |
|
Voir Programmation
|
|
||
|
Relations avec les valeurs précédentes
Surprenant relation avec e
Entier le plus proche (arrondis)
de factorielle n sur e = 2,718… ou partie entière (plancher)
de factorielle n sur 2 plus 1/2. Premier Le seul nombre premier les
sous-factorielles est 2. Rapport limite
|
Exemples avec la première formule
Avec les autres !4 = 3 x (!3 + !2) = 3 x (2 + 1) = 9 !4 = [4!/e] = [24 / 2,718] = [8,8] = 9 Probabilité d'un dérangement La probabilité qu'une permutation
choisie uniformément parmi toutes
les permutations soit
un dérangement est asymptotiquement égale à 1/e. |
|
![]()
|
|
||
|
Définition Nombres de dérangements (anglais: derangement numbers
or Montfort numbers). Permutation
des éléments d'un ensemble telle qu'aucun élément ne se retrouve dans sa
position initiale. Soit n un nombre entier naturel non
nul et E un ensemble de cardinal n. On appelle dérangement de E toute
permutation de E ne laissant aucun élément de E invariant. On dit aussi: permutation sans point fixe. Dénombrement (voir
tableau) Le tableau montre
les 24 permutations de quatre éléments (24 = 4!). En couleur ocre les
éléments qui occupent la même place qu'au départ. Encadrés en bleu (lignes
sans ocre), les 9 permutations "dérangées"; aucun élément n'est à
la place initiale. Notez que les
nombres en place (points fixes) apparaissent 6 = 3! fois dans chaque colonne. Exemples d'applications 1. Nombre
de manières de placer les
lettres dans les enveloppes de sorte que chaque lettre se trouve dans la
mauvaise enveloppe (adresses toutes différentes). Probabilité = 1/e
= 0,367… 2. Deux
jeux de cartes mélangés: probabilité qu'aucune correspondance n'existe, en
sortant les cartes deux par deux = 1/e = 0,367… 3. Cas des chapeaux à la sortie
d'une réception: aucun n'est sur la tête de son propriétaire. 4. Cas
des élèves qui notent les autres sans se noter soi-même. 5. Cas
de polyominos de certaines
dimensions. Historique Problème étudié en premier par Pierre de Montfort en 1708 et résolu
par lui et, simultanément, par Nicholas Bernoulli en
1713. Euler
(1707-1783) calcule les premiers termes et établit les formules de
récurrences. |
Permutations de quatre éléments
|
|
Voir Combinatoire
- Index
|
|
||
|
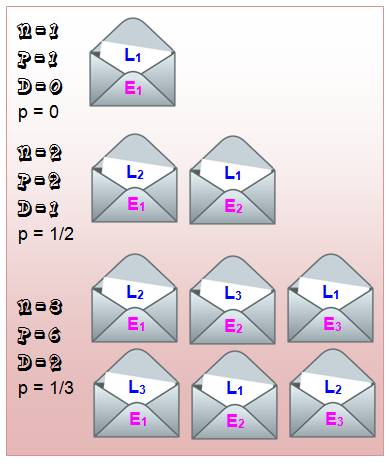
De
n = 1 à 3 Cas
des enveloppes et des lettres dont aucun n'est à sa place. Avec deux envois
(n = 2), deux possibilités (P = 2) pour mettre les lettres dans les
enveloppes dont une seule de se tromper (D = 1). La probabilité de se tromper
est p = 1/2. Avec
n = 3, deux possibilités de se tromper
pour 6 permutations des lettres dans les enveloppes. La probabilité
est p = 2/6 = 1/3. Pour
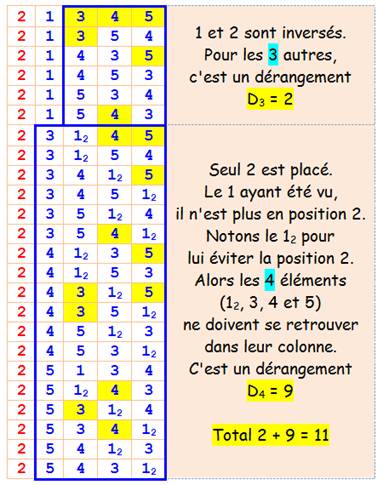
n = 5 Nous
savons que D5 = 44. Voyons comment le calculer (voir tableau). Première colonne Pas
de 1, bien entendu. Quatre
cas possibles: 2, 3, 4 et 5. Autant
de possibilités pour chacun d'eux. D5 = 4 x C Si première colonne = 2 Deux
situations à distinguer: les 1 et 2 sont simplement inversés sur leur
position, ou pas. Si première colonne = 2 et deuxième = 1 Les
trois autres (3, 4 et 5) doivent être dérangés sur les 3 colonnes (3, 4 et
5). C'est un dérangement d'ordre 3, et D3 = 2. Si première colonne = 2 et deuxième = (3, 4 ou 5) L'astuce est de considérer le 1 à placer
comme un pseudo-2. En effet, le 1 a déjà été placé en position 2 et ne doit
plus s'y trouver, c'est donc un faux 2, noté 12 dans le tableau. Alors,
les quatre valeurs (12, 3, 4 et 5) doivent être dérangées sur les
4 colonnes (2, 3, 4 et 5). C'est un dérangement d'ordre 4, et D4 =
9. Total pour colonne = 2, 3,
4 puis 5 C'est
quatre fois la valeur trouvée: D5 = 4
x (D3 + D2) = 4 x (2 + 9) = 44 Généralisation Le
même raisonnement peut se tenir non plus pour n = 5, mais pour n quelconque
et l'on obtiendrait: Dn =
(n – 1) x (Dn-1 + Dn-2) |
Cas n = 1, 2 et 3 – Exemple des
enveloppes
Cas n = 5 avec le 2 en première
colonne – Tableau et mise en évidence de deux
situations
|
|
|
Écrivons
la relation sous une autre forme qui met en évidence une relation de récurrence. |
|
|
|
En
descendant en valeur de n: |
|
|
|
En
revenant aux dérangements. Ou
en reprenant la notation des sous-factorielles. |
|
|
|
|
||
|
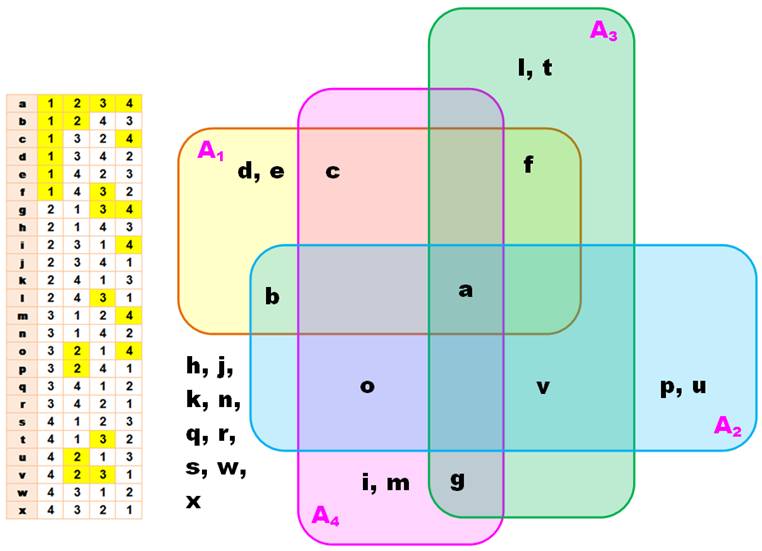
Avec l'exemple de
quatre éléments, A1 est le sous-ensemble des permutations
conservant le 1 en sa position; A2 conserve le 2 en sa position;
idem pour A3 et A4. |
Par exemple, les permutations notées d et e appartiennent
uniquement au sous-ensemble A1; par contre, la première permutation a appartient aux quatre
sous-ensembles. |
|
|
|
||
|
Ensemble
"coloré" = réunion des
quatre sous-ensembles |
Là, il existe au
moins un élément fixe (conservant sa position initiale) |
|
|
Sa négation (ou
toutes les permutations – celles "colorées" = |
Toutes les
permutations sans point fixe. |
|
|
Formulation: la quantité de
dérangements est égale au cardinal
de l'ensemble inverse (bar) de l'union de tous les sous-ensembles du type A1,
ceux qui conservent les éléments à leur place. |
Suite du
calcul sur Wikiuniversité >>> |
|
|
|
||
|
Théorème La
quantité de dérangements d'un ensemble comprenant n éléments est: |
|
|
|
Chapeaux Cas de
l'énigme des 10 chapeaux; calcul de la probabilité qu'aucun ne soit remis à
son propriétaire à la sortie de la cérémonie. |
|
|
|
Limite Cas d'un
nombre infini de chapeaux |
|
|
|
|
|
|
Subfactorial or rencontres
numbers, or derangements: number of
permutations of n elements with no fixed points. Subfactorial n (!n or a(n)) is the number of
desarrangements of length n. A desarrangement of length n is a permutation p
of {1,2,...,n} for which the smallest of all the ascents of p (taken to be n
if there are no ascents) is even. Source du
texte : OEIS A000166
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette
page |
![]()