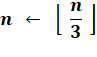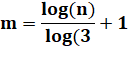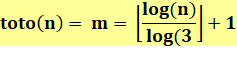|
|||||||||||||||||||||||||||||
![]()
|
Puissance de 3 Découverte d'un algorithme et réalisation de sa programmation. Explication pas à pas pour novice
dans ce domaine. |
Voir
Nombre 3
|
|
||
|
Problème Il s'agit
de découvrir l'algorithme indiqué:
Attention la compréhension de cet algorithme n'est pas si évident que cela ! |
Contexte Fonction: toto(n) qui retourne un entier Entrée : n, un nombre entier Sortie : entier ≥ 0 Algorithme
|
|
|
|
||
|
Algorithme Fonction toto(n) |
toto est le nom de la fonction que l'on pourra
appeler à loisir avec un programme principal. C'est en quelque sorte une
nouvelle instruction. |
|
|
Entrée: n est un entier Sortie: m est un entier |
Déclaration de deux variables n et m, deux nombres entiers tels que m = toto(n). |
|
|
|
Initialisation de l'algorithme avec m = 0. Plus exactement la
valeur 0 est placée dans une mémoire qui s'appelle m. On se souvient que n est déjà connu. Sa valeur a été introduite en
appelant la fonction toto. |
|
|
tant que n |
Lancement d'une boucle de calcul (on
dit: calcul itératif). Le principe est de
faire plusieurs fois le même calcul, mais avec des valeurs différentes, sous
réserve d'une condition. Ici, l'itération ne
sera exécutée que si n est plus grand ou égal à 1. La boucle s'arrête si n
passe en dessous de la valeur 1. |
|
|
|
Nous sommes dans le corps de la boucle. Le premier calcul consiste à prendre la partie entière de la division
de n par 3 (c'est ce que signifient les crochets par le bas). Pour information: les logiciels utilisent l'instruction plancher
(ou floor en anglais). |
|
|
|
La valeur de m est incrémentée de 1
(on ajoute 1 à m). En pratique, l'ordinateur va prendre la valeur de m lui ajouter 1 et
replacer cette valeur dans la mémoire nommée m. |
|
|
Fin de tant que |
La description de la boucle est terminée. Le calcul dans la boucle est
donc constitué de deux instructions:
|
|
|
Retourner m |
L'algorithme retourne la valeur de m. Le programme principal lui présente
un nombre entier n et l'algorithme termine son travail lui en fournissant la
valeur de m. Attention aux pièges. Pour bien comprendre ce qui se passe, mieux vaut suivre la trace de
l'exécution pour quelques valeurs. On pressent une histoire qui se passe tous les multiples de 3. Pas sûr
que l'on devine à ce stade, une histoire de puissance de 3. |
|
|
|
||
Prenons n = 1 Au départ: n = 1 et m = 0 On entre dans la boucle pour la première itération:
L'algorithme reprend son travail en début de
boucle et s'aperçoit que sa condition est remplie: n est inférieur à 1; il
stoppe la boucle. Et, il répond que m = 1. Prenons n = 6 Au départ: n = 6 et m = 0 Il faut deux itérations pour que l'algorithme
détecte le passage de n en dessous de 1. La réponse est
m = 2 ou encore toto(6) = 2 |
Deux exemples
|
|
|
Autres exemples Ci-dessous, on donne m (numéro de ligne) et les
valeurs successives de m pour les nombres indiqués.
Observations Notez les valeurs marquées en rouge: passage à la
valeur suivante de m pour les puissances
de 3: 3, 9, 27, 81, 243 … |
||
|
|
||
|
Interprétation En relevant la valeur de m pour les plages de
nombres n, on constate que, pour la plage des 3k , la
valeur de m est égale à k + 1. Ou dit autrement pour le nombre de tête de plage:
Fonction toto ? En passant aux logarithmes
Pour n quelconque,
on prendra la valeur entière de la fraction.
|
|
|
|
|
||
|
Programmation de la fonction
|
Commentaires La fonction toto est ici une procédure, abrégée
en proc. Le symbole On déclare que les variables m et n se seront
utilisées qu'en interne (local) à cette
procédure. On initialise m à 0 et n prend la valeur d'entrée
N. On conserve intacte la valeur d'entrée N, et on travaille sur n dans la
procédure. Tant que se dit while
en anglais et faire se dit do. On fermera
la boucle avec un do à l'envers. Calcul de n et de m sans problème (floor = plancher = nombre tronqué à sa partie
entière). Return enregistre que c'est bien la valeur de m
qu'il faut présenter en sortie de ce travail. Et une instruction end pour indiquer que l'écriture
de la procédure est terminée. |
|
|
Programme principal
|
Le programme principal va nous donner les valeurs
de m pour les nombres de 79 à 83 (par exemple). Nous lançons une boucle qui se lit: Impression à l'écran (lprint)
de:
Fin de l'écriture de la boucle avec do à l'envers. En bleu, le résultat du traitement. Nous trouvons
bien le même nombre pour le calcul de m avec la fonction toto et le calcul
direct avec notre formule. |
|
![]()
|
Retour Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
http://villemin.gerard.free.fr/aInforma/aAlgorit/Puissan3.htm
|
![]()