|
NOMBRES - Curiosités, théorie et usages Accueil / Dictionnaire / Rubriques / Index / Références / Nouveautés ORIENTATION GÉNÉRALE - M'écrire - Édition du: 10/05/2012 |
|
-Ý- FAQ - Foire
aux Questions |
||||
|
GÉOMÉTRIE |
/ Constructions |
|
|
|
|
>>>
ÉTOILES À 5 BRANCHES >>> SANS LEVER LE CRAYON >>> CENTRE DU CERCLE >>> CERCLE, CENTRE & 30° >>> CENTRE DU CERCLE – Méthode Napoléon |
Pages Générales § Théorie des
nombres - Index § Calcul § Logique § Humour |
|||
|
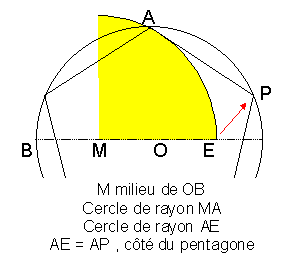
Rubrique OU PENTAGONE Question Construction
? Réponse
Voir suite et une autre méthode sur ma page en http://villemin.gerard.free.fr/Wwwgvmm/Geometri/CinqEtoi.htm |
|||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||
|
Rubrique Question Peut-on dessiner un carré avec une croix
dedans sans lever le crayon et sans repasser deux fois sur un trait Réponse A) La réponse est NON, c'est impossible Que la croix soit droite ou selon les diagonales Pour sauver la face, tu peux dire que c'est possible, mais au carré et diagonales, il faut ajouter deux traits au-dessus pour former une enveloppe: là, c'est possible et c'est même une devinette très célèbre B) La règle est assez simple (une fois connue) Pour chaque sommet, notez le nombre de traits qui y aboutissent Ce nombre est pair ou impair S'il y a 0 ou 2 sommets impairs, alors le tracé en un coups de crayon est possible Dans tous les autres cas c'est impossible C) Explication Si le nombre est PAIR, on peut toujours arriver au sommet et en repartir En présence d'un sommet IMPAIR, chaque fois que j'y arrive, je peux en repartir, sauf une fois. Pour ce dernier trait je suis bloqué. Pour que ce soit réalisable il faut exactement deux points de blocage: l'un est le départ et l'autre l'arrivée D) Voir explications, exemples célèbres (pont de Königsberg, enveloppe…) et un peu de théorie sur les chemins Eulériens en: http://villemin.gerard.free.fr/Wwwgvmm/Logique/DeuxEuler.htm |
|
|
|
|
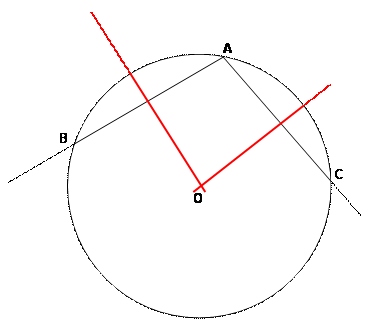
Rubrique CONSTRUCTION - CENTRE DU
CERCLE Question Le cercle est dessiné. On dispose d'une règle. Trouvez le centre du cercle Réponse À ma connaissance, ce n'est pas faisable dans ces conditions A) Première approche Pour que cela soit faisable, il faut admettre que la règle dispose d'une marque Ou ce qui revient au même: que l'on utilise la règle comme une unité de longueur
Ce que nous venons de voir est le principe de la construction avec des allumettes En utilisant le compas, on construit les médiatrices plus facilement B) Deuxième approche Avec une règle- équerre, il est possible de construire le centre encore plus facilement
C) Généralisation Tous les types de constructions (ceux-ci et d'autres) sont comparés en http://villemin.gerard.free.fr/Wwwgvmm/Geometri/Construc.htm#typecons Toutes les constructions de partage en n parts égales en http://villemin.gerard.free.fr/GeomLAV/Cercle/Partage.htm |
|||||||
|
|||||||
|
CERCLE, CENTRE & 30° Question Je suis paysagiste, je viens de réaliser une maçonnerie en pierre plate (dallage). Comprenant un cercle de 2 m de diamètre, avec 2 marches au bord du périmètre partant en spirale. Comment calculer ou trouver le point qui permet de tracer cette spirale. Comment trouver un angle de 30° dans ce même cercle. Réponse Voici quelques idées
|
|||||||||||||
|
|||||||||||||
|
CERCLE – Méthode Napoléon Question Trouver le centre avec un compas seulement
– Solution autre que celle des médiatrices Réponse C = centre; R = rayon
Merci à Maurice E. |
|||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||