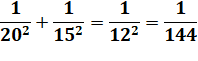Collection de nombres, théorème et triplets de Pythagore

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 04/11/2021 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Puissances
Débutants Pythagore Débutants Pythagore – Diaporama	Opérations sur les puissances		Glossaire Puissances
INDEX Triplets Puissances Partition	Somme de puissances
	Triplets de Pythagore	Th de Fermat-Wiles
	Démonstration du théorème	Carré somme de cubes
	Sommaire de cette page >>> Théorème de Pythagore >>> Le triangle rectangle le plus célèbre >>> Triplets de Pythagore >>> Propriétés des triplets >>> Détection des triplets >>> Triplets réciproques >>> Triplets colorés >>> Triplets – Index	Sur pages suivantes >>> Propriétés des triplets >>> Construction de triplets >>> Formule >>> Triplets primitifs >>> Illustration >>> Historique >>> TABLES

Pensées de Pierre Dac

Géométrie politique : le carré de l'hypoténuse parlementaire est égal à la somme de l'imbécilité construite sur ses deux côtés extrêmes.

Quand ça ne tourne pas rond dans le carré de l'hypoténuse, c'est signe qu'il est grand temps de prendre les virages en ligne droite.

Voir Pensées & humour

TRIANGLES RECTANGLES

TRIPLETS de PYTHAGORE

CARRÉ = SOMME DE 2 CARRÉS

Célèbre théorème utilisé par tous les géomètres

et par les maçons qui veulent s'assurer qu'un angle est droit.

Deux centres d'intérêts dans cette rubrique:

la démonstration du théorème: multiples versions; et

les triplets de trois carrés, l'un étant la somme des deux autres.

3² + 4² = 5²

33² + 44² = 55²

333² + 444² = 555²

…

Curiosité

5² + 12² = 13²

15² + 112² = 113²

Un doublet sans doute unique mais non prouvé – Robert Carman

(Les deux triplets sont primitifs)

Anglais: Pythagorean triangles and triples

Oups! Je suis débutant >>>

Petites devinettes

Seriez-vous capable de trouver x ?

Solution

Qui sont ces deux savants ?

Pythagore et Einstein

Voir Jeux et puzzles / Pensées & humour

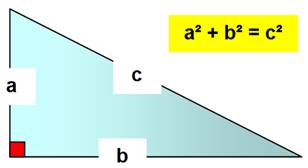
THÉORÈME DE PYTHAGORE

Triangle égyptien ou de Pythagore

Théorème de Pythagore

Dans un triangle rectangle, la somme des carrés des mesures des côtés de l'angle droit est égale au carré de la mesure de l'hypoténuse.

Plus vite dit:

La somme des carrés des côtés égale le carré de l'hypoténuse.

Réciproque

Un triangle présentant cette propriété est rectangle.

Pythagore - Biographie

Démonstrations

Fermat

Historique

L'équation diophantienne a² + b² = c² est associée à l'école de Pythagore (vers 570 av. J.-C.). Pourtant, les Babyloniens connaissaient la solution au moins mille ans avant.

Suite en Historique

Devinette

Alex est appelé à un concours de javelot en Corse. Le règlement est strict: pas d'objet de plus de 2 m à bord du ferry. Alex se voit refuser l'accès à bord du fait que son javelot réglementaire mesure 2,30 m. Trop long. Que faire?

Solution

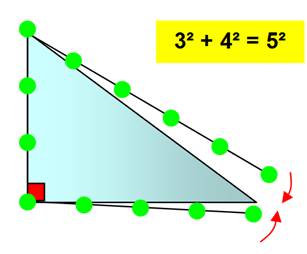
Le triangle rectangle le plus célèbre

3² + 4² = 5²

9 + 16 = 25

Le triangle du jardinier (ou du maçon ou de l'arpenteur)

Avec une ficelle comportant treize nœuds équidistants, il est possible de se passer d'une équerre pour tracer un angle droit.

Pour former un angle droit. les maçons multiplient chacun de ces trois nombres par 20. Ces valeurs 60, 80 et 100 en centimètres sont plus pratiques à mesurer.

Voir Construction de l'arpenteur

Extraordinaire! Le rayon du cercle inscrit à ce triangle, comme à tous les autres de Pythagore, est lui aussi un nombre entier >>>

Triangle rectangle

Belles formules

Nombres consécutifs

Différences de carrés

Triangle doré

Spirale du jardinier

Ellipse du jardinier

Triangle équilatéral avec 345

Illusion de l'œil de bœuf

TABLES de 1 à 500

Suite en Triangle isiaque

Propriété géométrique du triplet: 3 est triangulaire, 4 est carré, et 5 est pentagonal.

Le seul autre triplet de la sorte est: (100, 105, 145).

Voir Quelle est la hauteur de l'immeuble? Le triplet isiaque / Autres égalités, somme de carrés consécutifs

Aire (A) et périmètre (P)

Condition	Côtés	A	P	Commentaire
*A = 1/2 P*	3² + 4² = 5²	6	12	Seul
*A = P*	6² + 8² = 10²	24	24	Deux seuls
	5² + 12² = 13²	30	30	Deux seuls
*A = 2 P*	12² + 16² = 20²	96	48	Le plus petit
*A = 3 P*	20² + 21² = 29²	210	70	Le plus petit

Fibonacci

L'aire du triangle de Pythagore est un multiple de 6.

Théorème de Bachet

Aucun triangle pythagorique n'a une aire carrée >>>

Aire

Un triangle de Pythagore (i.e. rectangle à côtés entiers non nuls) possède toujours une aire entière.

Les côtés (x et y) du triangle rectangle sont de parités distinctes; l'un d'eux est pair. L'aire du triangle qui est le demi produit des deux (1/2 x.y) est bien un nombre entier.

Il n'existe pas de triangle de Pythagore dont l'aire est un carré ou le double d'un carré.

The area of a Pythagorean triangle cannot be the square or twice the square of a natural number.

Carré

Il n'existe pas de triplets tels que a et b soient eux-mêmes des carrés.

Périmètre

Triangles

Triangles avec triplets

Propriétés

TRIPLETS de PYTHAGORE

Triplets de Pythagore

Toutes les solutions en nombre entiers de l'équation a² + b² = c² est un triplet de Pythagore.

Autres noms

Triade pythagorique.

Triangle pythagorique.

(a, b ,c) sont des entiers pythagoriciens.

Définition

Un triplet d'entiers strictement positifs

(a, b, c)

est dit pythagoricien

si (a, b, c) est solution de

l'équation de Pythagore.

Triplets

Nombres congruents

Carrés

Équation de Pythagore

Équation diophantienne

X² + Y² = Z²

dont la solution générale est:

X = u² - v²

Y = 2 u.v

Z = u² + v²

u et v sont des entiers.

Suite en

Construction des triplets

Voir

Équation

Équation diophantienne

Équations équivalentes

a² + b² = c²

(a/c)² + (b/c)² = 1

x² + y² = 1

x et y étant des fractions,

des nombres rationnels.

Trouver les triplets de Pythagore

revient à

Trouvez tous les points

à coordonnées rationnelles

sur le cercle de rayon unité.

Suite >>>

(0,8)² + (0,6)² = 0,64 + 0,36 = 1

Illustration

Nombres rationnels

Racines de l'unité

Propriétés des triplets de Pythagore

Autres propriétés (certaines ne sont pas encore démontrées)

L'hypoténuse (c) d'un triplet primitif est de la forme 12k + 1 ou 12k + 5.

Triplet quelconque, alors:

Triplet quelconque (a, b, c) avec a et c premiers et a > 10 alors y est divisible par 60.

Triplet quelconque (a, b, c) avec a et c premiers, alors le triplet est de la forme (p, (p² - 1)/2 et (p² + 1)/2) avec p un premier impair.

Deux triplets (a, b, c) et (a', b', c') avec a>b>c et a'>b'>c', alors un de ces nombres est un carré: aa' (bc' – cb') ou aa' (bb' – cc').

Il n'existe pas de double triplets tels que a² + b² = c² et b² + c² = d²: côté et hypoténuse d'un triangle rectangle ne peuvent pas devenir deux côtés d'un triangle rectangle.

Suite en Propriétés des triplets avec démonstrations / Voir Divisibilité / Carré / Parité

Détection des triplets de Pythagore

par programmation

Trouver les carrés qui sont somme de deux carrés: a² + b² = c². Par exemple, le plus connu, car très joli:

3² + 4² = 5²

Nous mettons en place deux boucles: une pour dérouler a de 1 à 25 (par exemple) et l'autre pour b en partant de a jusqu'à 25. Inutile de partir de 1, nous aurions des doublons comme 3² + 4² = 4² + 3² = 5².

Après le calcul de la somme de leur carré (N:= a²+b²), nous en prenons la racine carrée (ou la puissance ½) et nous évaluons sa valeur décimale (evalf).

Pour détecter si ce nombre (RN) est une racine carrée exacte (un nombre entier) nous comparons ce nombre à la valeur entière de la racine (ERN:=floor(RN)). En fait, nous excluons les valeurs de RN qui ont des décimales (des chiffres après la virgule).

Nous pouvons ajouter un compteur pour dénombrer les triplets jusqu'à 1000, par exemple.
Le compteur (kt) est:

initialisé: kt:=0:

incrémenté à chaque fois qu'un triplet est détecté: kt:=kt+1:

imprimé en fin de programme: kt;

Jusqu'à 1000, il y a donc 1034 triplets.
Nous avons mis le signe # devant l'instruction d'impression des triplets pour éviter de lister à l'écran les mille valeurs. Ce signe permet d'introduire des commentaires dans le programme.

Avec notre programme, il est facile de chercher les sommes de deux cubes produisant un cube: a³ + b³ = c³.

Il n'y a en aucun et le théorème de Fermat-Wiles affirme que de tels triplets au cube n'existe pas, ni même à la puissance 4 et d'ailleurs pour aucune autre puissance que 2.

Ici, nous rencontrons un petit souci de calcul auquel il faut prêtre attention. La commande evalf en temps normal calcule avec une profondeur de dix décimales. Il est prudent d'en demander un peu plus. J'ai pris 20, en mettant la commande Digits:=20.

Voir Programmation / Maple

Triplets réciproques
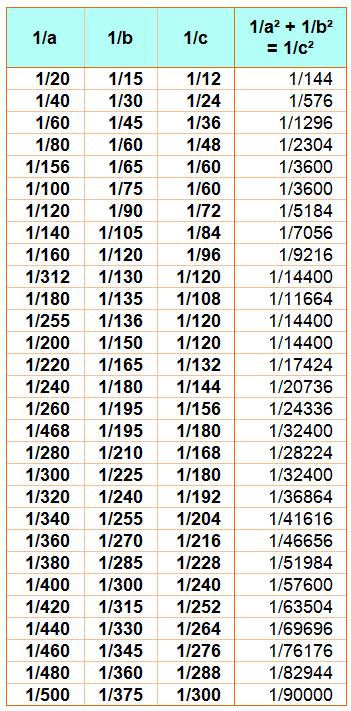
Triplets réciproques: somme des inverses des carrés	Exemple
Tableau Ils sont 29 pour a, b et c de 2 à 500. Le premier triplet du tableau se lit: Primitifs Certains sont simplement les multiples de triplets primitifs. Cas de 1/40, 1/60 ou 1/80, par exemple pour le triplet primitif en 1/20.

Triplets colorés

Attribuons une couleur aux nombres de façon telle que les trois nombres impliqués dans un triplet de Pythagore ne soient pas de la même couleur. Est-ce possible?

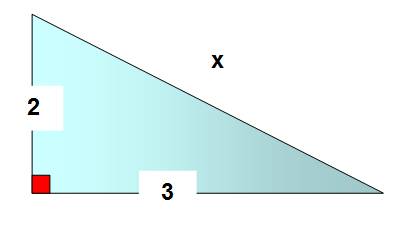
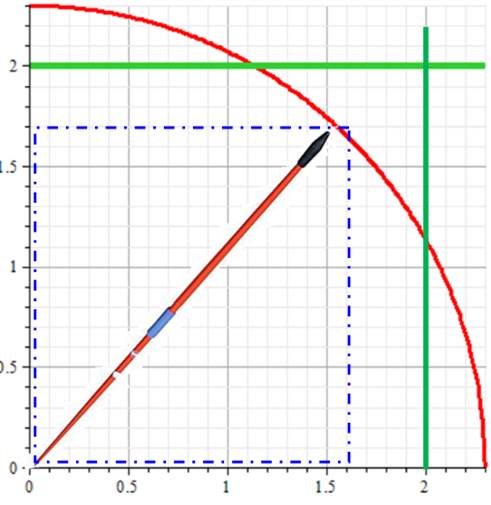
Voir Problème des nombres en couleurs

Trouvez x !

Eh bien, il est là, juste à la pointe de la flèche!

Retour

Devinette – Question et solution

Solution: il suffit emballer le javelot dans une boite rectangulaire. Alors; longueur et largeur seront moins grandes que la diagonale. Heureusement que la réglementation n'interdit pas les paquets volumineux!

Illustration: Graphe longueur en fonction de la largeur telle que la diagonale est égale à 2,3 m. Le javelot placé tient, par exemple dans une boite de 1,7 m x 1, 6 m (pointillés bleus)

En rouge: graphe y = racine (2,3² – x²)

Vérification avec le théorème de Pythagore pour la boite bleue:

1,7² + 1.6² = 5,45 = 2,33…² > 2,3 m.

Retour

Suite sur le théorème de Pythagore >>>

Suite sur les triplets de Pythagore

Introduction	Vision Juniors	Propriétés	Historique
Primitif	Génération	Matrice	Avec un carré
Illustration	Triangles	Briques	Spéciaux
Voisins	Moyenne quadratique		Cercle
Calculs	Extension vers Fermat-Wiles		Puissance 5
x² + y² = 2 z²	Triangles rectangles entiers		Triangle 345
Table 1 à 500	Différence = carrés (Rolle)		a² + b² + a + b = c² + c
Rayon du cercle inscrit (toujours un entier)
Points rationnels sur le cercle
Création d'une cascade de triplets par concaténation et retournement
Triangle rectangle et point interne à 3, 4 et 5 de distance des sommets
Heptagone de Pythagore: les sept triplets avec 24.

Voir	Théorème de Pythagore – Débutant Années Pythagore Calcul du facteur de Lorenz Décade de Pythagore Généralisation (Minkowski) Nombres premiers de Pythagore Pythagore - Biographie Somme de carrés Somme de carrés n fois Le théorème en 3D – Cas de la pyramide
Aussi	Addition - Glossaire Années Pythagore Bi, tripartitions Bouleversements et crises en maths Cercle Conjecture de Riemann Conjecture d'Euler Décade de Pythagore Équations diophantiennes – Liste Nombre = sommes de puissances Nombres carrés Nombres polygones Nombres triangles Partitions Petit théorème de Fermat Programmation de recherche des triplets Pythagore - Biographie Quadruplets diophantiens Somme de carrés Somme multi puissantes Théorie des nombres Triangle Triangle héronien Triangle isiaque Triplets de Markov Unité des puissances
Site	Pythagorean Right-Angled Triangles – Dr Ron Knott – 2018 – Site de référence sur les triplets de Pythagore, comporte un calculateur en ligne
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Addition/ThPythag.htm