|
Édition du: 12/01/2025 |
|
INDEX |
GRAPHES |
||
Faites
un double-clic pour un retour en haut de
page
![]()
|
CHEMIN ou GRAPHE EULÉRIEN Figures unicursales Un seul coup de cr |
||
|
|
Sommaire de cette page >>> Approche >>> Degré des
sommets >>> Chemin
eulérien >>> La
célèbre enveloppe >>> Le
célèbre pont de Königsberg >>> Passage de
frontière >>> Vocabulaire |
Débutants Glossaire |
Anglais : Eulerian graph
(path): a trail in a finite graph that visits every edge exactly once (allowing
for revisiting vertices).
|
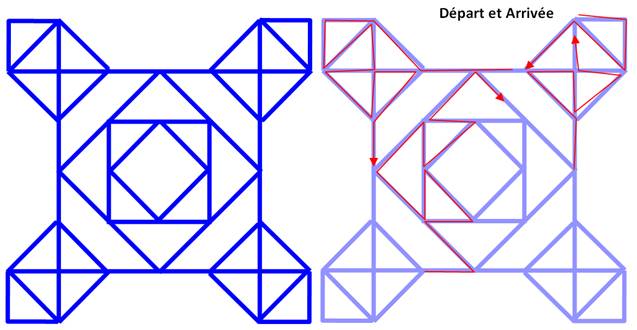
Dessinez
complétement cette figure sans lever le crayon. Pas si simple! Bonus:
pouvez-vous dessinez d'un seul trait une guérite (petite maison) avec sa
sentinelle (garde en arme) ? |
|
|
|
||
|
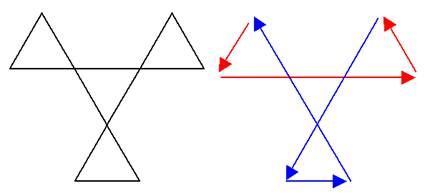
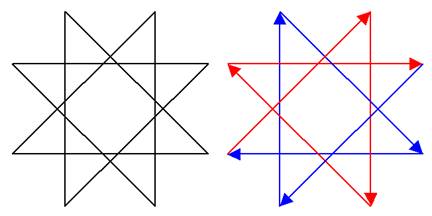
Pas de problème pour
dessiner ces deux figures sans lever le crayon. Croix de cauchemar Pas de problème non plus. Elle aurait une signification magique. |
|
|
|
Est-ce possible pour toutes les figures ? Non ! Voyez
l'exemple ci-contre. |
|
|
|
|
||
|
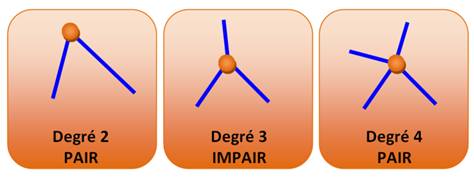
Un sommet est caractérisé par le nombre de segments qui
y concourent. On appelle ce nombre le degré du sommet. Le sommet est soit
de degré pair, soit de degré impair. |
|
|
Voir Pair
et impair
|
|
|||
|
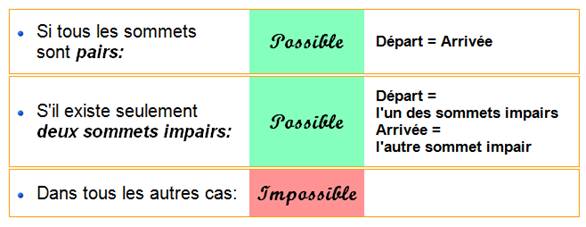
Chemin eulérien: graphe qui peut
être dessiné d'un seul coup de crayon, sans repasser sur un tracé. |
Règle
|
||
|
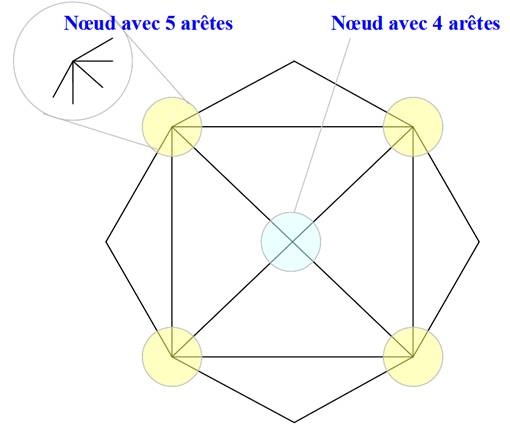
On remarque rapidement, en effet, que pour un degré 3: dans un sens comme dans l'autre,
impossible d'aller plus loin. Ces points sont des points de départ ou d'arrivée. |
|
||
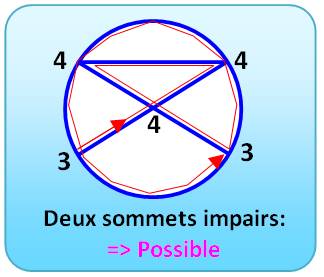
Le
cas du cercle à droite est équivalent au cas de l'enveloppe exposé ci-dessous
|
|
||
|
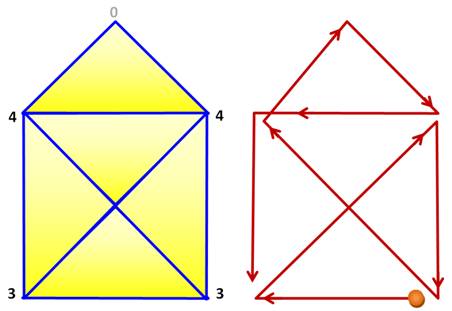
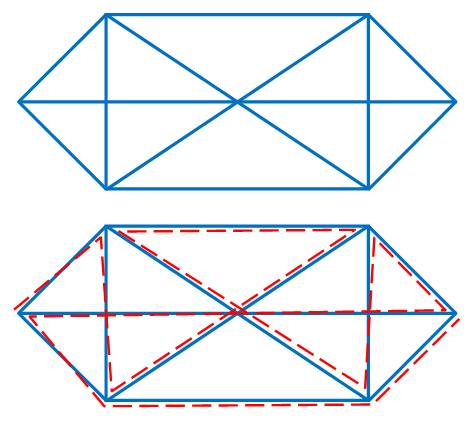
Dessinez l'enveloppe en un trait. Cette énigme est
apparue dans les livres de mathématiques en 1844. Nous notons deux sommets impairs, et seulement deux, le
tracé est donc possible. Notez que la pointe de l'enveloppe (0)
n'est pas un sommet. |
|
|
|
Réalisable Deux nœuds impairs aux extrémités gauche et droite. |
|
|
|
Réalisable
|
||
|
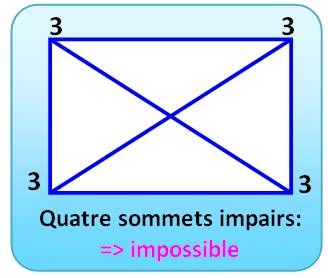
Irréalisable: quatre nœuds impairs
|
||
Voir Un
carré et deux triangles équilatéraux
|
|
||
|
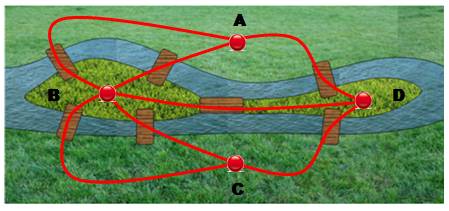
D'un
bord à l'autre Comment aller d'un bord à l'autre en passant une seule
fois sur chaque pont ? Essais Ce parcours (rouge) va bien du bord sud au bord nord,
mais en laissant de coté le pont central. Euler, qui vivait dans cette ville, a
montré que c'est impossible. (1736). Il donnait naissance à la théorie des
graphes. |
|
|
|
Cycle
eulérien Le graphe montre que tous les sommets (A, B, C et D)
sont impairs. Impossible d'aller d'un
bord à l'autre en utilisant les ponts chacun une seule fois. En
effet, Euler remarqua que, si un trajet existait, de chaque nœud partirait un nombre pair d'arêtes. Depuis,
un chemin d'un graphe partant et arrivant au même nœud, en passant une et une
seule fois par chaque arête est appelé un cycle
ou chemin eulérien. |
|
|
|
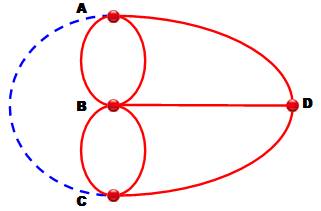
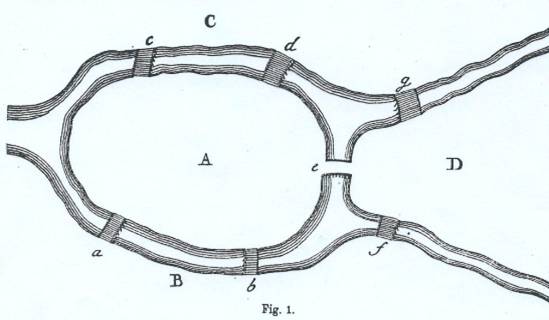
Graphe
topologique Le graphe
dessiné sur la figure ci-dessus peut agréablement se transformer en
celui-ci-contre. On peut le
déformer, tout en conservant la topologie
des chemins. Graphe
planaire Avec un
pont de plus entre A et C, (ici,
positionné à gauche et représenté sur le graphe par un pointillé bleu)
alors un tracé en un seul coup de crayon serait réalisable en partant de D et
en arrivant en B. Dans ce
cas, le graphe est dit planaire. |
|
|
Voir Énigmes juniors / Brève
n°393
Dessin original
|
Pendant son séjour à l'Académie des sciences de
Saint-Pétersbourg, Euler reçut une lettre curieuse. Elle provenait de la
ville pittoresque de Königsberg en Prusse (Kaliningrad dans la Russie
actuelle). Morcelée par les bras de la rivière Pregel, la ville consistait en
quatre quartiers séparés reliés par sept ponts. Le maire de la ville voisine
de Dantzig, Carl Leonhard Gottlieb Ehler, voulait organiser un circuit à pied
de Königsberg de telle manière que les touristes franchissent tous les ponts.
(…) Le grand mathématicien fut d'abord réticent. (…) Il
n'existait en fait dans toute la science mathématique aucun instrument qui puise s'attaquer à une énigme de ce
type. (…) Certes, le philosophe allemand Gottfried Wilhem Leibniz (1646-1716) et son élève
Christian Wolf (1679-1745) avaient suggéré une nouvelle discipline
mathématique, qu'ils baptisèrent analysis situs
(…) Euler montre qu'il est carrément impossible de parcourir
Königsberg à pied de la manière souhaitée (…) et donne les conditions exactes
dans lesquelles une ville dotée d'îles et de ponts peut être parcourue de la
manière prescrite. |
Extrait de La conjecture de Poincaré – George G.
Szpiro – Lattès Points sciences – 2007 – pages 85 à 87
|
|
||
|
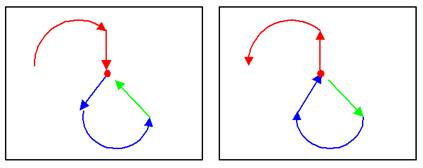
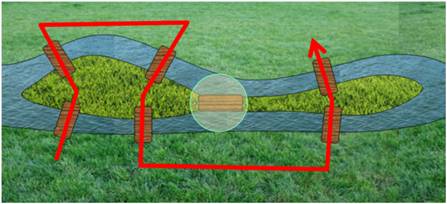
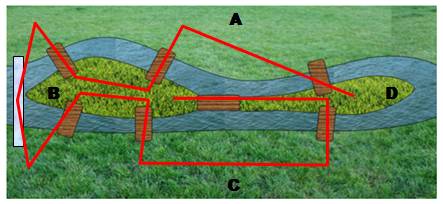
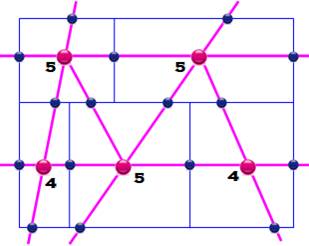
Un pays
et ses frontières. Comment passer par toutes les frontières une seule fois? L'essai
en vert est infructueux. Reste la frontière rouge à traverser. Impossible. |
Avec une telle
figure, passer par toutes les frontières semble impossible. |
|
|
Ce
problème est du même type que le précédent une fois le graphe équivalant
construit:
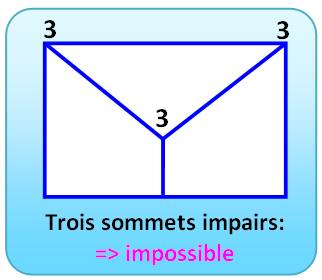
Ce graphe
comporte trois sommets impairs. Le parcours eulérien est impossible. |
La parité des
sommets du graphe équivalent montre que le parcours est impossible. |
|
|
|
||
|
Page
déplacée |
||
|
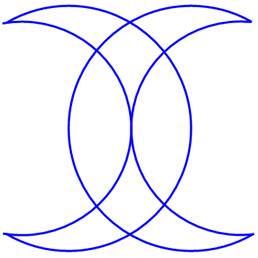
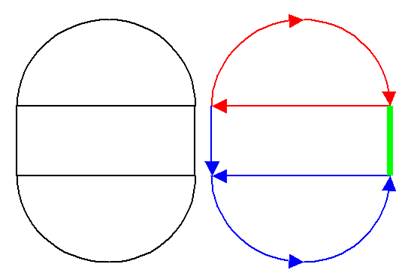
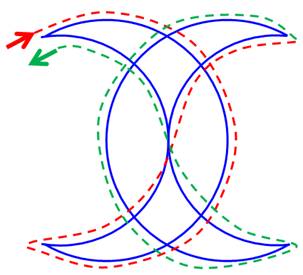
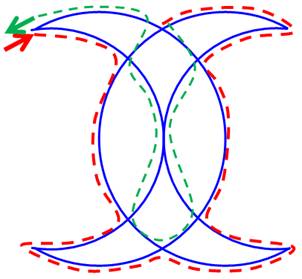
Les deux demi-lunes enchevêtrées Remarquez
que tous les sommets sont pairs. Ce qui veut dire que la solution est
possible. Suivez
le trait rouge puis le trait vert. L'astuce, en haut, consiste, après un demi-cercle, à
prendre un chemin qui croise les deux demi-lunes. L'astuce, en bas, consiste à suivre l'extérieur puis
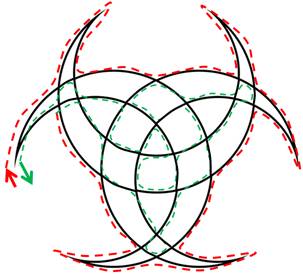
l'intérieur. Les trois demi-lunes (ci-dessous) La
solution systématique (extérieur, puis intérieur) s'applique sans difficulté. |
Solution élégante
Solution systématique
|
|
|
|
|
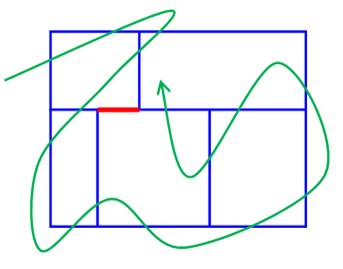
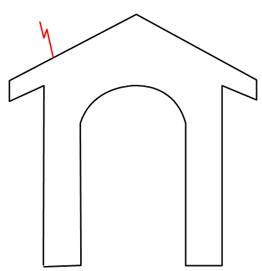
La guérite et la sentinelle Vous
dessinez ce croquis en commençant par la partie rouge qui semble être une
erreur de dessin. Votre
ami vous interroge: mais où est la sentinelle? – Elle est derrière la
guèrite. Seul le bout de sa baïonette dépasse! |
|
Voir Lunules / Lune / Les gardes du
fortin
![]()
|
|
|
Voir Index complet et mis à
jour
|
|
||
|
|
||
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Logique/DeuxEuler.htm |
|