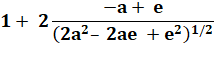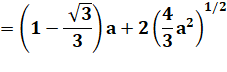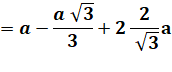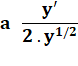|
Édition du: 08/03/2024 |
|
INDEX |
GRAPHES |
||
Faites
un double-clic pour un retour en haut de
page
![]()
|
CHEMIN LE PLUS COURT Comment concevoir des réseaux de distribution les plus courts entre
villes ? |
||
|
|
Sommaire de cette page >>> Plus court
chemin >>> Villes
disposées en carré >>> Calcul de la dérivée |
Débutants Glossaire |
|
|
||
|
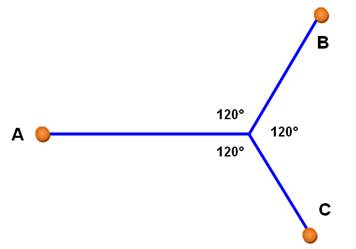
Trois points
Voir Cas du triangle équilatéral |
|
|
|
Quatre points
|
|
|
|
|
|||
|
|
|
||
|
|
|
||
|
Fonction à étudier: |
L(e) = |
e + 2 (2a² – 2ae + e²)1/2 |
|
|
Sa dérivée: |
L'(e) = |
|
|
|
Maximum pour une dérivée
nulle. Mis au carré: |
2(a – e) = 4(a – e)² = |
|
|
|
Nouvelle équation: |
0 = |
3e² – 6 ae + 2a² |
|
|
Dont les solutions sont: Solution la plus petite
retenue. |
e = |
|
|
|
Soit pour L: |
L = |
e + 2 (2a² – 2ae +e²)1/2 |
|
|
Intermédiaire de calcul: |
2a² – 2ae +e² |
= 4/3 a² |
|
|
Reprise de L: L = 2, 73 a alors qu'avec la solution diagonale L = 2,83 a |
L |
=2,732… a |
|
|
|
||||
|
|
L(e) = |
e + 2 (2a² – 2ae + e²)1/2
|
||
|
En pratique et en
gros, tous les termes descendent d'un degré et les exposants se retrouvent en
facteurs. |
||||
|
Exemple |
a xr |
|
a r xr – 1 |
|
|
Ici |
e 2a² – 2ae + e² |
|
1 0 – 2a + 2e. |
|
|
|
||||
|
Exemple |
a y1/2 |
|
|
|
|
Ici, dérivation par rapport à e: |
(2a² – 2ae + e²)1/2 |
|
|
|
|
Et pour L(e) |
L'(e) |
= |
|
|
Voir Autre exemple de dérivée avec
racine
Bilan
|
Nous
venons de voir le cas de trois ou quatre points. Le problème se complique
énormément avec plus de quatre points. Voir le cas du voyageur
de commerce. |
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()