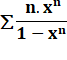fonctions génératrices des nombres entiers

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 25/01/2018 Orientation générale DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Partitions
Débutants Algèbre	Fonctions GÉNÉRATRICES				Glossaire Partition
INDEX Partition	Introduction	Nombres entiers	Diviseurs	Principales FG
		Partitions
		Sommaire de cette page >>> Diviseurs

FONCTIONS GÉNÉRATRICES

des DIVISEURS des NOMBRES

Une fraction simple engendre tous les nombres entiers. Existe-t-il une fraction qui donne la somme des diviseurs de tous les nombres à la suite?

OUI, mais la formule se complique juste un petit peu. Voyons cela pas à pas…

Diviseurs
	1, 2, 2, 3, 2, 4, 2, 4, 3, 4 …	Quantité des diviseurs des nombres successifs – Lambert 1771	>>>
	1, 3, 4, 7, 6, 12, 8, 15, 13, 18 …	Somme des diviseurs des nombres successifs – Euler 1747	>>>
	1, 3, 4, 7, 6, 12, 8, 15, 13, 18 …	Somme des puissances k des diviseurs des nombres successifs

Pour comprendre ces formules, voir le développement complet sur les partitions

Suite

Voir

Cette page