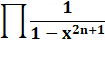NOMBRES - Curiosités, théorie et usages

 

Accueil                           DicoNombre            Rubriques           Nouveautés      Édition du: 25/01/2018

Orientation générale        DicoMot Math          Atlas                   Références                     M'écrire

Barre de recherche          DicoCulture              Index alphabétique       Brèves de Maths    

            

Partitions

 

Débutants

Algèbre

Fonctions GÉNÉRATRICES

 

Glossaire

Partition

 

 

INDEX

 

Partition

 

Introduction

Nombres entiers

Diviseurs

Principales FG

Partitions

 

Sommaire de cette page

>>> Rappel – Fonction génératrice

>>> TABLE systématique 1er et 2e degrés

>>> TABLE des fonctions remarquables

 

 

 

 

 

 

 

FONCTIONS GÉNÉRATRICES

 

Répertoire des principales fonctions génératrices des suites de nombres.

 

Entier, impair, carré, cube, somme de diviseurs …

 

 

Rappel – Fonction génératrice

 

Fonction génératrice des entiers:

 

 

À l'exemple de cette fonction, les tableaux ci-dessous donnent:

*      le numérateur et le dénominateur de la fonction génératrice;

*      la valeur de coefficients de la série infinie; et

*      le type de suite de nombres que la fonction engendre.

 

Exemple de présentation

1

/

(1 – x)2

1, 2, 3, 4, 5 …

Suite des entiers positifs

 

En bleu, les fonctions qui produisent des suites remarquables.

 

Division de 1 par (1 – x)²

 

Voir Division de polynôme

 

 

TABLE SYSTÉMATIQUE

pour le premier et le deuxième degré

Numérateur

/

Dénominateur

Suite

Nom

Lien

1

/

1 – x

1, 1, 1, 1, 1 …

Suite de 1

>>>

1

/

1 + x

1, -1, 1, -1, 1 …

Suite alternée de 1 et -1

 

1 + x

/

1 – x

1, 2, 2, 2, 2 …

Suite de 2 après le 1 initial

>>>

1 + x

/

1 + x

= 1

 

 

1 – x

/

1 – x

= 1

 

 

1 – x

/

1 + x

1, -2, 2, -2, 2 …

Suite alternée de 2 et -2  après le 1 initial

 

1

/

(1 – x) ²

1, 2, 3, 4, 5 …

Suite des entiers positifs

>>>

1

/

(1 + x) ²

1, -2, 3, -4, 5 …

Suite alternée des entiers positifs et négatifs

 

1 + x

/

(1 – x) ²

1, 3, 5, 7, 9 …

Suite des entiers impairs

>>>

1 + x

/

(1 + x) ²

= 1 / (1 + x)

 

 

1 – x

/

(1 – x) ²

= 1 / (1 – x)

 

 

1 – x

/

(1 + x) ²

1, -3, 5, -7, 9 …

Suite alternée des nombres impairs

 

x

/

(1 – x) ²

0, 1, 2, 3, 4, 5 …

Suite des entiers positifs avec 0 au départ

 

x

/

(1 + x) ²

0, 1, -2, 3, -4, 5 …

Suite alternée des entiers avec 0 au départ

 

x²

/

(1 – x) ²

0, 0, 1, 2, 3, 4 …

Entiers avec deux 0 au départ

 

x²

/

(1 + x) ²

0, 0, 1, -2, 3, -4, 5 …

Entiers alternés avec deux 0 au départ

 

1 – x²

/

(1 – x) ²

= (1 + x) / (1 – x)

 

 

1 – x²

/

(1 + x) ²

= (1 - x) / (1 + x)

 

 

(1 + x)²

/

(1 – x) ²

1, 4, 8, 12, 16, 20 …

Un suivi des multiples de 4

>>>

(1 + x)²

/

(1 + x) ²

= 1

 

 

(1 – x)²

/

(1 – x) ²

= 1

 

 

(1 – x)²

/

(1 + x) ²

1, -4, 8, -12, 16 …

Un suivi des multiples de 4 alternés

 

 

 

TABLE des FONCTIONS REMARQUABLES

Numérateur

/

Dénominateur

Suite

Nom

Lien

Entiers et figurés

 

 

 

1

/

(1 – x) 2

1, 2, 3, 4, 5, 6 …

Nombres entiers positifs

>>>

1

/

(1 – x) 3

1, 3, 6, 10, 15, 21 …

Nombres figurés triangulaires
(ordre 3 – somme des entiers)

>>>

1

/

(1 – x) 4

1, 4, 10, 20, 35, 56 …

Nombres figurés tétraédraux
(ordre 4 – somme des triangulaires)

>>>

1

/

(1 – x) 5

1, 5, 15, 35, 70, 126 …

Nombres figurés pentatope 
(ordre 5 – sommes des tétraédraux) )

>>>

1

/

(1 – x) k

1, k, (k² - k(k-1)/2 …

Nombres figurés d'ordre k
(somme des figurés d'ordre k-1)

>>>

Impairs, carrés …

 

 

 

1 + x

/

(1 – x) 2

1, 3, 5, 7, 9 …

Nombres entiers impairs

>>>

1 + x

/

(1 – x) 3

1, 4, 9, 16, 25, 36 …

Carrés
(somme des impairs)

>>>

1 + x

/

(1 – x) 4

1, 5, 14, 30, 55, 91 …

Pyramide carrée
(somme des carrés)

>>>

1 + x

/

(1 – x) 5

1, 6, 20, 50, 105, 196

Somme des pyramides carrées

 

1 + x

/

(1 – x) k

1, k+1, (k+3)k/2 …

Somme de tels nombres de rang k-1

 

x(1+x)

/

(1 – x) 3

0, 1, 4, 9, 16, 25, 36 …

Carrés avec 0 au départ

 

x² + 4x + 1

/

(1 – x) 4

1, 8, 27, 64, 125, 216 …

Cubes

>>>

x (x² + 4x + 1)

/

(1 – x) 4

0, 1, 8, 27, 64, 125, 216 …

Cubes avec 0 au départ

 

x3+11x²+11x+1

/

(1 – x) 5

1, 16, 81, 625, 2401 …

Puissances 4 des nombres

>>>

Multiples

 

 

 

 (1 + x)²

/

(1 – x) 2

1, 4, 8, 12, 16, 20 …

Un suivi des multiples de 4

>>>

Puissances

 

 

 

1

/

1 – 2x

1, 2, 4, 8, 16, 32 …

Puissances de 2

>>>

1

/

1 – 3x

1, 3, 9, 27, 81, 243 …

Puissances de 3

>>>

1

/

1 – 4x

1, 4, 16, 64, 256, 1024 …

Puissances de 4

>>>

1

/

1 – k.x

1, k, k², k3  …

Puissances successives de k

>>>

1 + x

/

1 – 2x

1, 3, 6, 12, 24, 48 …

Trois fois une puissances de 2

 

Fibonacci & Lucas

 

 

 

1

/

1 – x – x²

1, 1, 2, 3, 5, 8, 13 …

Nombres de Fibonacci

>>>

1

/

1 – 2x – x²

1, 2, 5, 12, 29, 70, 169 …

Nombres somme de deux fois le précédent
et une fois celui d'avant (12 = 2x5+2)

 

1

/

1 – k.x  - h.x²

1, k, h+k², 2hk+k3 …

Nombres de Fibonacci généralisés
tels que an = k.an-1 + han-2

 

1 + 2x

/

1 – x – x²

1, 3, 4, 7, 11, 18, 29 …

Nombres de Lucas

>>>

 

Diviseurs

 

 

 

1, 2, 2, 3, 2, 4, 2, 4, 3, 4 …

Quantité des diviseurs des nombres successifs
 – Lambert 1771

>>>

1, 3, 4, 7, 6, 12, 8, 15, 13, 18 …

Somme des diviseurs des nombres successifs
 – Euler 1747

>>>

1, 3, 4, 7, 6, 12, 8, 15, 13, 18 …

Somme des puissances k des diviseurs
des nombres successifs

 

Partitions

 

 

 

1, 2, 3, 5, 7, 11, 15, 22, 30 …

Quantité de partitions propres d'un nombre
(Hors cas identiques par permutations)

>>>

0, 1, 0, 2, 0, 3, 0, 5, 0 …

Avec seulement des nombres pairs

 

1, 1, 2, 2, 3, 4, 5, 6, 8 …

Avec seulement des nombres impairs

 

1, 1, 1, 1, 2, 2, 2, 3, 3 …

Avec seulement des carrés

 

 

 

 

 

 

Suite

*         Fonctions génératrices – Nombres entiers

*         Tables des FG classiques

*         Fonctions génératrices des partitions

Voir

*         Suites

*         Fractales

Cette page

http://villemin.gerard.free.fr/Wwwgvmm/Suite/FoncTabl.htm