|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
SUITES et SÉRIES Suite:
famille de
nombres, souvent indexés par les entiers naturels: U1, U2
…Un … ; Si n n'est pas limité, alors la suite est infinie; Elle est
récurrente si le suivant est calculé à partir du (ou des) précédents: Un+1
= f(Un). Série: suite de termes, chacun étant la somme (cumul) des termes successifs d'une suite. |
Voir DicoMots Maths – Suites et Séries /
Évaluation de CM1
|
Saucisses Chaussettes Cuites Pont-Neuf Édifice Quelle est la suite? |
Patates, ou Bronze, ou Viaduc de Millau. |
|
|
|
|
Vous avez une suite
de nombres. Vous vous
demandez ce qu'elle représente et quels sont les nombres suivants. Consultez le site: séquence de nombres
sur OEIS
(The on-line encyclopedia of integer sequences) Vous aurez
quasi-sûrement la réponse. |
|
|
|
|
|
U TTT CCCCC SSSSSSS NNNNNNNNN Quelle
est la suite? OOOOOOOOOOO Pourquoi?
Il s'agit de la première lettre des nombres impairs successifs, autant de
fois que le nombre qu'elle représente. |
|
|
Anglais: look-and-say
sequence |
|
|
Une suite
mystérieuse 1 11 21 1211 111 221 ?..
La clé du mystère
Voir suite en Séquences
numériques |
|
Voir Compter
les blocs de "1" ou de "0" / Nombres
auto-descriptifs
|
|
||
|
Suite des nombres
triangulaires 1 , 3 , 6 , 10 , 15 , 21 , ...
Nn
= n (n + 1) / 2 |
||
|
Empilement de billes 1 1
+ 2 = 3 1
+ 2 + 3 = 6 1
+ 2 + 3 + 4 = 10 Intersection de n
droites 2
droites => 1 point d'intersection 3 => 3 points 4 => 6 points |
|
|
|
|
|
|
Suite des nombres
quantité d'empilements de cubes 1 , 2 , 4 , 8 , 16 , ..
|
|
|
|
|
|
Suite des nombres
quantité d'empilements de cubes en escalier 2 , 5 , 14 , ...
|
|
|
|
|
|
Suite des esters de
carbone: 1 , 4 , 10 , 25 , 64 , 172 , ...
|
|
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
|
Trouvez la suite des nombres:
Il s'agit de la
quantité de lettres. |
|||||||||||||||||||||||||||||||||
Voir Suite EBAN
|
|
||
|
2, 3, 3, 5, 10, 13, 39, 43, 172, 177 |
On fait successivement: +1, x1, +2, x2, etc. Les suivants: 885, 891, 5346, 5353, 37471, 37479,
… |
|
|
0, 0, 0, 0, 4, 9, 5, 1, 1, 0, 55, ... |
Voir Nombre jeux avec chiffres
romains |
|
Source: Puzzle
Sequences from OEIS
|
|
|
|
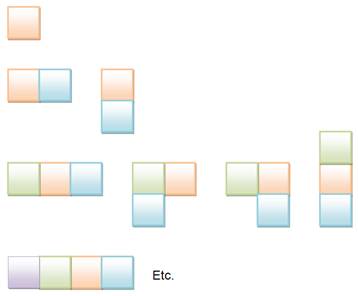
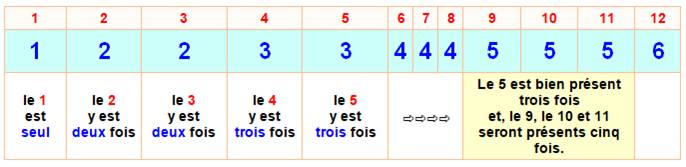
Définition Le
nième nombre dans la suite est le nombre de fois que l'entier n est dans la
suite. La
suite 1, 2, 2, 3, 3, 4,
4, 4, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 8, 8, 8, 8, 9, 9, 9, 9, 9, 10, 10, 10,
10, 10, 11, 11, 11, 11, 11, 12, 12, 12, 12, 12, 12 … Sa
lecture
Commentaires Cette
suite est la plus petite croissante. Formule
de récurrence: a(1) = 1 a(n+1) = 1 + a(n +
1 – a(a(n))) La
valeur asymptotique de la suite est liée au nombre
d'or:
|
|
|
|
|
|
Définition La
suite et la suite constituée des différences contiennent tous les nombres une
seule fois. La
suite 1, 3, 7, 12, 18,
26, 35, 45, 56, 69, 83, 98, 114, 131, 150, 170, 191, 213, 236, 260, 285, 312,
340, 369, 399, 430, 462, 495, 529, 565, 602, 640, 679, 719, 760, 802, 845,
889, 935, 982, 1030, 1079, 1129, 1180, 1232, 1285, 1339, 1394, 1451, 1509,
1568, 1628, 1689 … Sa
lecture
Le
1 est dans la suite. J'essaie
le 2. Sa différence avec 1 est 1; nombre déjà dans la suite. Le 2 est
éliminé. J'essaie
le 3. Sa différence avec 1 est 2; ce nombre n'est ni dans la suite ni dans la
suite des différences, il est élu. J'essaie
le 4, puis le 5, puis le 6; ils produisent tous des différences déjà dans la
suite et dans la suite des différences (nombres ne rouge). Le
nombre 7 est élu car il produit une différence égale à 4 pas encore en rouge.
Il attendre le 12 pour avoir une nouvelle différence égale à 6. Etc. Commentaires Suite
donnée par Hofstadter en 1980. Présentée dans le magazine Pour la Science en
1998. Introduite dans l'encyclopédie de séquences
d'entiers par Sloane et Plouffe. |
|
|
en
théorie des nombres |
|
|
Suite quantité de
diviseurs propres 0, 1, 1, 2, 1, 3, 1, 3 …
|
|
Devinette – Lire les nombres cachés …
|
Saucisses Chaussettes Cuites Pont-Neuf Édifice Quelle est la suite? |
Bronze, ou
|
D'après une énigme posée à un jeu télévisé
![]()
|
Suite |
|
|
|
Voir |
|
|
|
|
||
|
Cette page |
||
![]()