|
|||||||||||||||||||||||||||||
![]()
|
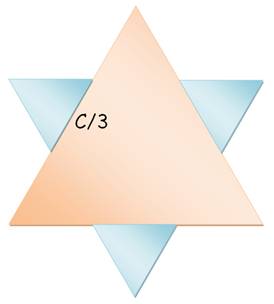
COURBES de Koch ou flocon de neige Calcul de l'aire de cette figure. Elle
finie alors que la longueur de la courbe est
infinie. |
Anglais: Area of the
Koch Snowflake
|
|
||
|
|
3 côtés
donneront naissance à 3 nouveaux triangles plus petits. |
|
|
|
||
|
C1 = 1/3 C
|
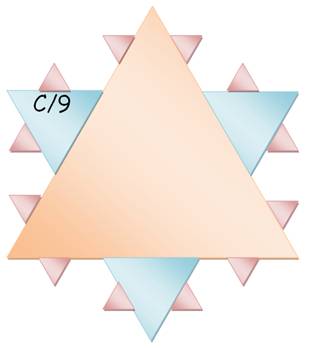
Les 3 nouveaux
triangles forment 3 x 4
arêtes = 12 qui donneront naissance à 12 triangles plus petits.
|
|
|
|
||
|
C2 = 1/3 C1 = 1/9 C
|
Les 12 nouveaux triangles forment 12 x 4 arêtes = 48 qui donneront naissance à 12
triangles plus petits. |
|
|
|
||
|
C3 = 1/3 C2 = 1/33
C
|
|
|
|
|
||
|
|
C1 = 1/3 C C2 = 1/3 C1 = 1/32
C C3 = 1/3 C2 = 1/33
C .. Cn+1 = 1/3 Cn = 1/3n C |
|
|
|
k = 1 k1 = 3 k2 = 4k1
= 4 x 3 k3 = 4k2
= 42 x 3 … kn+1 = 4kn
= 4n-1 x 3 |
|
|
|
|
|
|
|
n Hn An 1 1/3 0,
5773502693 2 4/27 0,
6415002993 3 16/243 0,
6700114236 4 64/2187 0,
6826830346 5 256/19683 0,
6883148615 6 1024/177147 0,
6908178958 7 4096/1594323 0,
6919303555 8 16384/14348907 0,
6924247820 9 65536/129140163 0,
6926445271 10 262144/1162261467 0,
6927421916 |
|
|
||
|
|
|
|
|
|
||
|
|
|
|
![]()
|
|
||
|
|
Commentaires On précise la taille au départ. Le bloc
(sous-programme) KOCH est exécuté
trois fois avec rotation de 120°. Ce bloc dessine les quatre lignes d'un motif du
flocon, en divisant chaque motif par 3, et en faisant appel à lui-même pour
descendre en finesse. En fin de boucle, le programme commande une avance
d'une longueur adaptée à la taille pour dessiner le motif suivant. Toujours impressionnant de voir la récursivité à
l'oeuve.
|
|
|
Répétition du flocon avec finesse progressive
La figure est faite en donnant la taille 5 au départ |
|
|
Voir Programmation – Scratch / Flocon dessiné avec Python
![]()
|
Retour Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette
page |
![]()