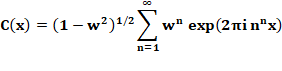|
|||||||||||||||||||||||||||||||||||
![]()
|
FRACTALES – Introduction
En zoomant une partie, le tout refait son
apparition.
Le même objet est observable même en
augmentant l'échelle.
|
Poupées russes ou en anglais:
Matryoshka russian nesting dolls
|
Je crois que le
savoir scientifique a des propriétés fractales, quelle que soit l'étendue de
nos connaissances, ce qui en reste, aussi petit que cela paraisse, est aussi
infiniment complexe que la totalité
l'était au début. Voilà, je crois le secret de l'Univers. Isaac Azimov Cité par Clifford Pickover
– Oh, encore des nombres - Dunod |
Voir
Pensées & humour
|
|
||
|
Vocabulaire Fractal, fractale, adjectif: Une fractale, nom féminin La construction
d'une fractale est finalement assez simple. Définition Larousse fractal, e, als adjectif Objet fractal. Géométrie fractale. La nature offre de nombreux exemples de
formes présentant un caractère fractal : flocons de neige, ramifications
des bronches et bronchioles, des réseaux hydrographiques, etc. Définition Encarta Fractales, figures géométriques de structure
complexe dont la création ou la forme met en jeu des règles utilisant le
fractionnement. Les fractales sont à la base d’un nouveau système de
géométrie permettant de représenter des objets très irréguliers tels que les
reliefs montagneux, les amas galactiques ou les côtes rocheuses très
découpées. |
|
|
|
Définition Wikipédia On
nomme figure fractale ou "fractale" par substantivation de
l'adjectif (ou encore en anglais fractal), une courbe ou surface de forme irrégulière
ou morcelée qui se crée en suivant des règles déterministes ou stochastiques
impliquant une homothétie interne. Le terme « fractale » est un néologisme
créé par Benoît Mandelbrot en 1974 à partir de la racine latine fractus, qui
signifie brisé, irrégulier. Dans la « théorie de la rugosité » développée par
Mandelbrot, une fractale désigne des objets dont la structure est liée à
l'échelle. Ma définition Objet
géométrique obtenu par exploration du comportement d'une fonction en chaque
point d'un plan (par exemple). Sa représentation graphique montre des formes
esthétiques qui se reproduisent quelle que soit l'échelle de représentation
(autosimilarité ou homothétie
interne). |
||
Voir Réflexions sur
les fractales
|
|
||
|
Habituellement
|
Triangle
Cette seule zone agrandie ne permet pas de dire qu'elle provient d'un
triangle. Voir
introduction sympathique en |
|
|
|
Chaque disque est percé de deux disques, lesquels sont percés de deux disques,
lesquels sont percés … |
|
|
||
|
|
|
|
Exemples
![]()
|
Extrait de livre
résumant l'historique du concept de fractale
From Newton to Mandelbrot: a primer in
theoretical physics with fractals for the personal computer** – Dietrich Stauffer, Eugene Stanley – 1996 Traduction
|
Voir Platon / Kepler / Newton / Mandelbrot
|
|
|||
|
Euclide
d'Alexandrie vers 300
avant J.-C. |
Il définit la géométrie qui
va prévaloir durant les deux millénaires
à venir: droite ou courbe, sans point rugueux. Et, surtout, avec quatre types
de dimensions entières: 0 pour le point; 1 pour la ligne; 2 pour le plan; et,
3 pour les solides. |
||
|
Apollonius (vers-262
à -190)
|
|
||
|
Edmond
Halley (1656-1742) |
Il pense que les orbites
s'expliquent par la loi de l’inverse des carrés. |
|
|
|
Albrecht
Dürer (1471-1528)
|
En 1520, Il explique comment
construire ses pentagones dans livre: Instructions
pour la mesure, à la règle et au compas des lignes, plans et corps solides. Sierpinski reprendra cette figure. |
|
|
|
Johannes
Kepler
(1571-1630) |
Il se rend compte que les planètes ne
décrivent pas des cercles mais des ellipses. |
||
|
Isaac
Newton (1642-1727) |
Il développe le calcul infinitésimal
qui lui permet de modéliser le
mouvement des projectiles et des planètes. |
||
|
Gottfried
Leibniz (1646-1716) |
Il développe le calcul
différentiel dont la formulation est plus claire que celle de Newton et
lui vaudra de passer à la postérité. Vers 1700, il introduit la notion d'autosimilarité:
propriété d'une figure qui préserve une certaine symétrie malgré les
variations d'échelle. |
||
|
(1789-1857) et
son élève Karl
Weierstrass |
Ils expliquent le paradoxe des
infinitésimaux (voir le paradoxe d'Achille et la
tortue ou celui de la flèche de
Zénon d'Élée (vers -490 à -425). |
||
|
James
Clerk Maxwell
(1831-1879) |
Il établit les équations
électromagnétiques en faisant un usage magistral du calcul différentiel. |
||
|
Pierre-Simon
Laplace
(1749-1827) |
Il affirmait que cette méthode de
calcul permettrait de prédire tout le futur de l'Univers à condition de connaître la
position exacte de chaque particule. Tout se déduit de lignes plus ou moins
courbe présentant des inflexions, des nœuds... objets qui se prêtent au
calcul différentiel. |
||
Régularité
|
Jusque
là tout est régulier, même si on sait désormais maitriser des formes très
complexes à l'aide du calcul différentiel. En bref: les courbes ont une
tangente bien définie en chaque point: notion de pente, de gradient, de
dérivation. |
|
Thomas
Malthus (1766-1834) |
Il remarque que la population
augmente de façon exponentielle
alors que la production de la nourriture ne croissait que linéairement.
Avec une telle évolution, il prédit une famine inéluctable. En réalité, des
freins naturels à la croissance existent dès que la nourriture vient à
manquer. |
|
|
Karl
Weierstrass (1815-1897),
Georg
Cantor (1845-1918)
et Henri
Poincaré (1845-1912) |
Ils font naître une nouvelle
géométrie plus à même de décrire les aspects irréguliers et rugueux du monde. |
|
|
Karl
Weierstrass 1872
|
Il est le premier à mettre en
évidence une courbe uniquement constituée d'angles et qui, par conséquent,
résiste au calcul différentiel. Avec Cauchy, il développait un nouveau domaine
des mathématiques : l'analyse dont un des objectifs était la définition
précise des nombres et de la continuité. L'illustration
présente une courbe formée d'une sommation de courbes en cosinus: Ces
courbes monstrueuses sont qualifiées de pathologiques. La
fonction complexe de Weierstrass (pour information):
Elle est
continue, mais ulle part dérivable. |
|
|
(1854-1912)
|
Mathématicien, physicien et
philosophe des sciences, il montre qu'il est possible d'avoir une vision du
comportement de systèmes dynamiques complexes en se ramenant à des modèles mathématiques
assez simples. Il découvre une nouvelle forme de fractales émergeant de
l'exploitation d'équations non linéaires. Sans l'aide des ordinateur, il
passera à côté de la beauté de ces fractales. En 1897, il publie Vorlesungen uber die
Theorie der Automorphen Funktoren (Conférences sur la théorie de fonctions
automorphes). Y figure des dessins du pavage hyperbolique que Esher
va reprendre (illustration). |
|
|
Pierre
François Verhulst (1804-1849) |
Dans les années
1840, mathématicien belge, il introduit une rétroaction négative dans le
modèle de Malthus. Ce modèle conduit à u e stabilisation de la population
selon la nourriture disponible. C'est l'équation logistique: xN+1 = R . xN (1 – xN) |
![]()
Les prémisses
|
Georg
Cantor (1845-1918)
|
Il est l'un des pionniers de la théorie
des ensembles. Il va se heurter toute sa vie à l'infini et à la nature du
continuum. En
1877, il découvre qu'il est possible de désigner un point du plan avec un
seul paramètre. Cantor disait: Je le vois, mais je ne le crois pas! En
1883, Cantor trouve un ensemble qui porte son nom et qui est de nature
fractale (Anglais: Cantor dust, poussière de Cantor).
Ensemble qui avait déjà été mis en évidence en 1875 par Henry Smith (1826-1883),
un professeur de géométrie à Oxford. Avec
sa fameuse diagonale,
il montre qu'il existe plus de points dans le continuum (nombres réels)
que ne peuvent en compter les nombres
naturels (nombres entiers). Il est contraint d'envisager l'existence de
plusieurs sortes d'infinis.
C'est l'arithmétique des transfinis. |
|
|
Giuseppe
Peano (1858-1932)
|
En 1890, professeur d’analyse
infinitésimale, il découvre une courbe qui remplit l'espace. Elle se replie
de façon telle qu'elle passe par chaque point du plan entier. Aucun point du plan
n'est exclu de la ligne courbe de Peano : cartographie biunivoque entre
une ligne et le plan. |
|
|
David
Hilbert (1862-1943)
|
David Hilbert crée sa courbe
pathologique, une courbe qui remplit l'espace (space filling curve). Un courbe
qui est de dimension 1 et qui remplis complètement un espace de dimension 2. |
|
|
Jean
Perrin (1870-1942) William
Feller (1906-1970) |
Perrin: physicien et chimiste français,
il publie Les atomes en 1913. Feller: mathématicien spécialiste
des probabilités. Einstein
publie en 1905 son explication théorique du mouvement
brownien en fonction du mouvement aléatoire des molécules. Jean Perrin
vérifie les prédictions d'Einstein et démontre en 1908 un accord complet
entre théorie et expérience, ce qui confirme l'existence effective des atomes. Feller
simule aussi le mouvement brownien et lui trouve une nature chaotique. |
|
|
Luitzen
Brouwer
(1881-1966) |
En 1911, mathématicien néerlandais,
il démontre que la dimension est un invariant
topologique ; elle ne peut pas être altérée par une déformation
continue. |
|
|
Paul
Lévy (1886-1971)
|
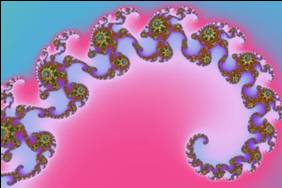
Mathématicien
français, un des fondateurs de la théorie moderne des probabilités. A
contribuée à la théorie du mouvement brownien. Son livre: Processus
stochastiques et mouvement Brownien. Il
décrit les propriétés de l'autosimilarité et en montre la construction
géométrique. Courbe décrite avant par Ernesto Cesaro (1906) et par Georg
Faber (1910). L'illustration
montre la courbe auto-similaire de Levy ou courbe en C. |
|
|
Gaston
Julia (1893-1929) étudiant de Poincaré et Pierre
Fatou (1878-1929)
|
Vers 1914, ils
étudient séparément la cartographie (ou transformation)
du plan des nombres
complexes par application de fonctions itératives. La transformation produit
une image d'un point de départ. Les
deux mathématiciens s’intéressent particulièrement aux images répétées
(itérations). Travaux méconnus car les résultats ne sont apparents que par le
grand nombre de points et le grand nombre d'itérations, impossible à révéler
sans l'aide des ordinateurs. Leurs travaux mettent en évidence des bassins
d'attraction aux frontières très compliquées connues sous le nom d'ensemble
de Julia. Gaston
Julia publie ses travaux en 1918: Mémoire sur l'itération des fonctions rationnelles.
Il y met en évidence ce qui est connu aujourd'hui sous le nom d'ensembles de
Julia: des bassins d'attraction aux frontières très tourmentées. Il les
imagine mais ne les verra jamais faute de disposer de moyens de calcul comme
les ordinateurs. Julia devient célèbre, mais ses travaux attendront cinquante
ans avant d'être exploités. Fatou
découvre exactement les mêmes résultats que Julia. Ce dernier lui disputera
l'antériorité. Bilan:
l'Académie des Sciences accorde le Grand prix à Julia et remet un prix
spécial à Fatou qui, découragé, fuyait la polémique, et n'avait pas voulu
concourir. |
|
|
Felix
Hausdorff
(1869-1942) |
Mathématicien allemand, père de la topologie
moderne, en 1919, il définit une nouvelle manière de considérer la notion de
dimension : la dimension fractale prenant des valeurs non entières. Son travail sera approfondi par
Abraham Samilovitch Besicovitch entre 1934 et 1937. |
|
|
Helge
von Koch (1870-1924)
|
En 1904, il invente la courbe flocon de neige ou courbe
triadique de Koch. La
courbe finale est infiniment longue bien que contenue dans un espace fini.
Elle ne possède aucune tangente et ne présente aucune régularité. En
pratiquant une coupe en des endroits précis on met en évidence une quantité
infinie d'ensembles de Cantor. La courbe de Koch contient quatre copies de la
courbe de Koch à l'échelle 1/3 ; sa dimension est log4/log3 = 1,26... |
|
|
Robert
Brown (1773-1858) |
En 1927, ce botaniste écossais,
découvre le mouvement brownien et sa
nature physique et non biologique. En 1906, Albert Einstein et Marian
Smoluchovski développe la théorie |
|
|
Jean
Perrin (1870-1942) |
Physicien et chimiste français, il démontre
en 1895 que les rayons cathodiques sont composés de corpuscules, les
électrons. Concernant le mouvement brownien, il
pense que la trajectoire est non-dérivable et qu'elle est auto-similaire. |
|
|
En 1926, il s’intéresse à la mesure
de la longueur
des côtes britanniques. Elle dépend de la taille de la règle. Elle est
infinie avec une règle infiniment petite. En fait, elle est fractale. |
||
|
Edward
Lorenz (1917-2008)
|
Mathématicien et météorologue du MIT,
il est le fondateur de la théorie du
chaos. À partir des données de Richarson, Mandelbrot en déduit que la
dimension fractale de la côte est d'environ 1,26. |
|
|
Vaclav
Sierpinski (1882-1969)
|
En 1916, Vaclav Sierpinski
(1882-1969), propose une nouvelle fractale : le joint de culasse ou
tamis de Sierpinski. Une figure dont le principe de construction était connu
de certains artistes comme Maurits Cornelis Escher
(1898-1972). Il consiste évider un triangle
équilatéral en son centre avec un triangle quatre fois plus petit. Les
trois triangles pleins sont évidés à leur tour. Bilan : une forme
composée de trois copies d'elle-même, chacune correspondant à la moitié du
trou. D'autres motifs peuvent être obtenus à partir d'autres polygones
et même polyèdres.
À notez : le triangle de Sierpinski se retrouve dans le triangle
de Pascal. |
|
|
Karl
Menger (1902-1985)
|
Mathématicien autrichien, en 1926,
il décrit la fractale en trois dimensions dite éponge de Menger (ou
Sierpinski-Menger). Extension en trois dimensions de l'ensemble de Cantor ou
du tapis de Sierpinski. |
|
|
Années 1970 |
La redécouverte de la formule d'itération quadratique de Verhulst va relancer la
théorie du chaos. Selon la valeur de R, tout va changer : convergence
vers une valeur, oscillation entre deux valeurs ; ou plusieurs ; ou
chaos. |
|
|
Rober
May (né en
1936) Mitchell
Feigenbaum (né en
1944) Feigenbaum = figuier en allemand
|
Vers 1970, Rober May découvre la
nature fantasque de la loi logistique. Avec R qui augmente, soudain, de
convergente (R < 2,6), la formule laisse place à une oscillation entre deux
valeurs, puis quatre avec R vers 3,1. Ce dédoublement
périodique est appelé bifurcation et va se renouvelle en continuant à faire
croître R. Le graphe représentant ces
bifurcations à la forme d'un figuier. C'est le graphe de Feigenbaum
(physicien américain). Il montre que la formule devient chaotique, puis ouvre
une fenêtre ou règne à nouveau l'ordre. |
|
|
Jackson
Pollock (1912-1956)
|
Ce peintre américain de
l'expressionisme abstrait est connu pour tableau fractals. L'analyse
montre que le principe d'autosimilarité statistique est respecté. Elle consiste à vérifier par
l'intermédiaire d'une grille de N carrés posée sur la toile que la proportion
de motifs reste constante quel que soit le nombre de carrés étudiés et donc
quelle que soit la taille des carrés. Illustration
avec le tableau Kaleidoscope flower. |
|
![]()
La vraie naissance des fractales
|
Benoît
Mandelbrot (1924-2010) Mathématicien
polonais franco-américain.
Voir sa programmation
simple avec Scratch |
En 1975 , il
invente le mot fractal. Du latin fractus,
brisé, cassé, fracturé.Il est considéré comme le père de la géométrie
fractale. The history of fractals dates back to 1975, when Fractals
were discovered by Benoît Mandelbrot. Il travaille chez IBM et résout un
problème de bruit aléatoire dans les transmissions entre ordinateurs. Il
avait constaté que les erreurs étaient de type fractal. Il prend connaissance
des œuvres de Julia et Fatou et les exploite à l'aide d'ordinateurs. Il
s'intéresse à une itération particulièrement simple : un nouveau point Z
du plan complexe est calculé en prenant le carré du
précédent ajouté d'une constante. ZN+1
= ZN2 + C Il
découvre de nombreuses figures (dragon auto-carrés) selon la valeur de la constante.
Ces figures sont soit totalement connectées (courbes fermée, boucles,
dendrites) ou totalement déconnectées (comme l'ensemble de Cantor). En
1980, Mandelbrot étudie les frontières entre ces deux types de figures. Julia
savait que l'ensemble est connecté si l'orbite d'un point durant une
itération est convergente et déconnectée si l'orbite se prolonge à l'infini.
Cette manière de cartographier le plan révèle la fameuse figure du pou
de Mandelbrot représentant l'ensemble M de Mandelbrot. Il y découvre avec
émerveillement que la grande figure se réplique sans fin à plus petites
échelles. Partant
d'une situation quelconque, Mandelbrot observe qu'à la longue, les points
sont attirés par une attracteur
dit étrange ou plus exactement un attracteur fractal. |
|
|
Tien
Yien Li et James
York en 1975 |
En 1975, ils
publient Period Three implies Chaos (la période trois entraîne le chaos) qui
introduit le terme de chaos puis le
développement d'une nouvelle science la théorie du chaos. Ces
deux auteurs montrent qu'un système dynamique à une dimension, avec un cycle
de période trois,
contient aussi toutes les autres périodes. Alexei
Sarkowski avait lui aussi, fait ce constat, passé inaperçu car écrit en
russe. Voici
un nouveau domaine où il faut admettre qu'il existe des choses que nous ne
pourrons jamais connaître, comme le principe
d'incertitude d'Heisenberg ou encor le théorème
d'incomplétude de Gödel. |
|
|
Mitchell
Feigenbaum En 1977 |
Il montre que le rapport entre les distances
entre bifurcations converge vers une constante
4,669 201 609 102 990 671 853 203 82... Le principe du doublement de période
est un principe général naturel. |
|
|
Michel
Barnsley (né en
1946) & Alan
Sloan |
En 1987, ils découvrent une autre
façon de construire les fractales. Il développe une méthode de compression
de l'information fractale basée sur la détection de récurrence de motifs. |
|
|
Kenneth
Falconer 1990 |
Il publie: Fractal Geometry: Mathematical
Foundations and Applications, une référence en matière de mathématique des
fractales. Seconde édition étendue en 2005. |
|
|
Tan
Lei (1963-2016)
|
La mathématicienne chinoise,
travaillant à l’université d'Angers, a prouvé que l'ensemble M de Mandelbrot
est asymptotiquement semblable aux ensembles de Julia proches d'un quelconque
point de sa frontière. Plus on zoom plus, la figure ressemble à un ensemble
de Julia particulier. |
|
|
Mitsuhiro
Shishikura (né en
1960) |
En 1998 (publication), le
mathématicien japonais démontre que la frontière de l’ensemble de Mandelbrot est
de dimension fractale 2, propriété conjecturée par Mandelbrot et Milnor. |
|
|
L'ensemble de
Mandelbrot n'est pas une invention. C'est une découverte. Un peu comme le
mont Everest
est juste là. Roger Penrose Demain, quelqu'un
qui n'est pas familiarisé avec les fractales ne pourra être considéré comme
scientifiquement instruit. John Archibald
Wheeler (1911-2008) - Physicien expert en cosmologie et en physique
quantique ; proche de Niels Bohr et
Albert Einstein Les fractales sont
importantes car elles ont permis de révéler un tout nouveau domaine des
mathématiques, pertinent directement pour l'étude de la nature. Ian Stewart,
professeur de mathématiques de l'université de Warwick en Angleterre. |
|
|
|
|
J. R. Maddocks
Wikipedia
Math Forum |
|

![]()

![]()
|
Suite |
|
|
Voir |
![]()
|
Livres |
|
|
Sites sélectionnés par TANGENTE |
|
|
Autres Sites |
|
|
Générateur |
|
|
Théorie |
|
|
Sites connexes |
|
|
Cette
page |
![]()