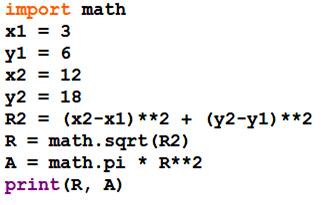|
Édition du: 11/10/2025 |
|
INDEX |
Python – Comment se lancer et initiation |
||
Faites
un double-clic pour un retour en haut de
page
![]()
|
PROGRAMMATION PYTHON – Les classiques Mes premiers programmes classiques en langage
Python. Occasion d'expérimenter les listes, les dictionnaires, les fonctions,
la récursivité. |
||
|
|
Sommaire de cette page >>> Exemple amusant avec les lettres >>> Simple addition avec entrées >>> Aire du disque à partir des coordonnées du
rayon >>> Addition dans une liste >>> Factorielle et récursivité >>> Fibonacci |
Débutants Glossaire |
Voir absolument Mon espace de travail
en Python
|
|
||
|
m i s |
Commentaires Programme qui détecte les lettres communes dans
deux mots. Définition de la fonction lettres communes (lc). Boucle d'exploration des lettres (L) contenues dans le mot a. Si cette lettre est aussi dans le mot b, imprimer cette lettre. Appel de la fonction lc
avec les mots mister et miss. Les lettres (m, i et s) sont bien présentes dans
le mot miss. |
|
|
|
||
|
|
Commentaires Demande d'entrée de deux nombres au clavier (input). Somme des deux nombres en décimal (float). Sortie (print)
avec texte. Notez le format pour inclure des variables dans le texte. Le symbole "\"
indique que l'instruction se poursuit sur la ligne suivante. |
|
|
|
||
|
Rédaction directe
15.0 706.8583… |
Commentaires Appel du module math. Introduction des coordonnées des extrémités du
rayon. Calcul de la longueur avec le théorème
de Pythagore: d'abord R², puis R. Notez comment on calcule la racine en rappelant
l'appel à math. La puissance s'exprime par **. Calcul de l'aire Notez la manière d'appeler la constante Pi. Demande d'impression du rayon et de l'aire |
|
|
Rédaction avec définitions
15 706.8583… |
Commentaires Il s'agit d'une rédaction qui définit des
fonctions. De la sorte, les programmes sont réutilisables pour toute autre
application. Définition du rayon avec les coordonnées de ses
extrémités Calcul de la longueur du rayon. Définition de l'aire du cercle à partir des
coordonnées des extrémités du rayon. Calcul de l'aire. Avec a = aire (…), on appelle la fonction aire
instanciées de valeurs numériques. On a demandé l'impression du rayon (15) et de
l'aire du cercle (706,85…) Il suffit de rappeler ces dernières instructions
pour calculer l'aire d'autres cercles. |
|
|
|
||
|
Rédaction détaillée
10 |
Commentaires Définition de la fonction somme de tous les nombres dans la liste L. Initialisation du total (T
= 0). Boucle en k
pour chacun des éléments de la liste L. Somme du kième élément au total tel qu'il existe. Notez la manière d'additionner (de cumuler) avec +=. Exemple avec: 1 + 2 + 3 + 4 = 10 |
|
|
Rédaction concise
15 |
Python dispose d'une fonction somme. |
|
|
|
|||
|
Version classique
120 |
Rappel Factorielle
(5) = 5! = 1 x 2 x 3 x 4 x 5 = 120 Commentaires Boucle qui multiplie F en cours par le pointeur k en cours. Pour bien commencer la multiplication F est initialisé à 1. |
||
|
Version avec définition d'une
fonction avec récursivité
720 |
Rappel de la définition récursive d'une factorielle 0! = 1 n! = n (n – 1) ! Commentaires Définition de la fonction factorielle du nombre n. Si n est nul dire que 0! = 1 (return). Sinon,
calcul de la factorielle du nombre précédent Notez l'appel à la fonction elle-même. On nomme
ce procédé en "poupées russes", la récursivité. Résultat L'appel à cette fonction pour le nombre 6 donne
bien: |
||
|
Version compacte
|
Commentaires Les instructions sous else sont
compactées en une seule instruction. On en profite pour monter comment mettre une boucle sous une seule
instruction. Le programme affiche les factorielles de 5 à 10 (non inclus).
|
||
|
Version compacte ultime
(copiable) def factorielle(n): return 1 if (n==1 or n==0) else n * factorielle(n-1); #exemple n = 10 print(f"{10} ! = {factorielle(n)} ") 10 ! = 3628800 |
|||
|
|
||
|
Rédaction directe
[0, 1,
1, 2, 3, 5, 8, 13, 21, 34, 55] |
Rappel de la définition de la suite de Fibonacci F(0) = 0, F(1) = 1 F(n) = F(n – 2) + F(n – 1) Commentaires Initialisation des deux premières valeurs à 0 et 1,
y compris pour la liste L. Déclaration d'un variable temporaire c. Boucle de neuf répétitions du calcul dans c du nombre de Fibonacci. Noria avec a, b et c
pour préparer le prochain calcul. Ajout (append) du nouveau Fibonacci (c) ) la liste L. Impression de la lite des Fibonacci. |
|
|
Rédaction avec récursivité
55 |
Commentaires Définition de la fonction Fibonacci
de rang n. Initialisation des premières valeurs si n = 0
puis si n = 1. Dans les autres cas, calcul du nouveau Fibonacci
à partir des deux précédents, lesquels sont calculés à partir des deux
précédents, …. jusqu'à ce que les deux précédents soient e rang 0 et 1 dont
les valeurs sont connues. Appel à la fonction pour le 10e
Fibonacci, qui vaut 55. |
|
|
Rédaction avec dictionnaire
55 144 |
But Le procédé par récursivité est impressionnant,
mais il a un inconvénient: les calculs sont recommencés à chaque fois. La procédé utilisant le dictionnaire mémorise les calculs déjà effectués
et accélère le calcul lors des appels suivants. Commentaires Initialisation du dictionnaire (FiMem). Notez les accolades. Définition de la fonction Fibonacci. Si la valeur est déjà mémorisée dans FiMem, retourner cette valeur. Sinon, procéder au calcul comme précédemment,
mais la recherche des précédents s'arrêtera dès qu'ils seront trouvés dans le
dictionnaire FiMem. |
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()