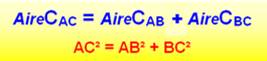Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 14/01/2024 M'écrire Brèves de Maths

INDEX Triangles Géométrie Puissances	Théorème de Pythagore
	Débutants	Nomenclature – Types de démonstrations		Applications
	En quatrième	Approche	Calcul Aires	Dissections
	Toute figure	Historiques	Similitudes	Hypoténuse
	Triplets de P.	Chinoise (Chou Pei)	Algébrique	Pyramide
	Pappus-Clairaut		Approximation de Pi

Théorème de Pythagore Approche et types et démonstrations Avec le théorème de Thalès, c'st le théorème le plus utilisé durant les études de secondaire. Il existe une collection des 370 démonstrations! Parmi elles, nombreuses sont de simples variantes. Ce théorème était connu des Babyloniens et des Chinois, bien avant Pythagore.
	Sommaire de cette page >>> Illustration du théorème de Pythagore >>> Illustration physique >>> Preuve simpliste – Cas particulier >>> Démonstration de Bhaskara >>> Démonstration par échange de triangles >>> Types de démonstrations et liens >>> Généralisation du théorème de Pythagore >>> Curiosités et brique de Pythagore	Débutants Géométrie Glossaire Géométrie

Anglais: Pytaghoras Theorem / Inde: Gougu theorem

Voir Bienvenue aux Internautes de l'éducation nationale

Voir Théorème de Pythagore et Théorème de Thalès – Débutants

Théorème de Pythagore en bref – Trois visions à retenir

Voir Démonstration de l'inverse du théorème de Pythagore

Notez les faux-amis anglais

Théorème de Pythagore – Illustration		haut
47^e proposition d'Euclide dans Les Éléments: Dans un triangle rectangle ABC: aire du carré construit sur l'hypoténuse = somme des aires des carrés construits sur les côtés. , Devinette Un cas très particulier d'application du théorème de Pythagore. Un lanceur de javelot voyage avec son engin de 2,40 m de long. Comment s'y prend-t-il pour prendre l'avion, sachant que l'aéroport n'accepte aucun colis de plus de 2,20 m de long? Solution	Figure des "moulins à vent" Cette illustration représente bien la manière de penser courante à cette époque, non pas en carré de valeurs mais surface. Voir Propriété de cette figure

Voir le Dab de Pogba

Illustration physique		haut
Il s'agit en fait d'une expérience astucieuse de travaux pratiques en physique qui illustre le théorème de Pythagore. Il s'agit du principe du sablier, ici, avec de l'eau. Les deux carrés* posés sur les côtés du triangle rectangle sont remplis d'eau. En basculant le "sablier" l'eau se déverse dans le grand carré accolé à l'hypoténuse. L'eau contenue dans les deux petits carrés remplit exactement le grand carré. Remarque * En fait, le dispositif est en volume, mais l'épaisseur étant constante, elle est neutre dans le calcul. Va + Vb = Vc a².e + b².e = c².e a² + b² = c² Notez que a².a + b².b = c².c a^3 + b^3 = c^3 est impossible.

Source images à partir de la vidéo: Pythagorean Theorem Water Demo - senorgif.com

Preuve simpliste (cas particulier)		haut
Preuve simpliste avec le triangle isocèle rectangle (jaune): Aire des deux petits carrés bleus = aire du grand carré vert = quatre triangles dans chaque cas. Les petits triangles isocèles rectangles sont identiques car ce sont des copies du triangle jaune central, avec les mêmes longueurs de côtés.

Démonstration de Bhaskara

haut

Sans doute la démonstration la plus simple, d'origine indienne (védique) et variante due au mathématicien indien Bhaskara (né vers 1114).

Première démonstration

On évalue la surface S du grand carré de deux manières:

Grand carré	S = (a + b)² = a² + 2ab + b²
Ses composantes	S = c² + 4 (ab/2) = c² + 2ab
Conclusion	=> a² + b² = c²

Deuxième démonstration (variante)

On évalue toujours la surface S du grand carré de deux manières:

Grand carré	S = c²
Ses composantes	S = 4 (ab/2) + (b – a)²
Conclusion	=> c² = a² + b²

Voir Découpe du rectangle

Démonstration par échange de triangles		haut
Construire les deux carrés jaunes de côtés a et b. En reportant le petit carré dans le moyen (pointillés), on trace la ligne rouge qui engendre deux triangles rectangles identiques de côtés a, b et c. Ces deux triangles déplacés en position bleue forment le grand carré oblique de côté c. Démonstration due à Thabit Ibn Qurra (vers 900). On retrouve cette disposition dans de nombreuses variantes

Voir Suite en dissections / Brève 433

Types de démonstrations			haut
Démonstrations historiques	Babylone, Chine, Inde >>> Bhaskara >>> Pythagore >>> Liu Hui >>>	Chou Pei >>> Thabit ibn Qurra >>> Euclide >>> Léonard de Vinci >>>
Démonstrations par dissections Puzzles	Simpliste >>> Découverte >>> Liu Hui >>> Thabit ibn Qurra >>> Dissection à deux triangles >>>	Dissection de Perigal >>> Dissection à quatre triangles >>> Dissection à sept et huit pièces >>> Dissection de Dudeney >>> Chou Pei >>>
Démonstrations par calcul des aires	Bhaskara >>> Euclide >>> Léonard de Vinci >>> Mascheroni-Président Garfield >>> Dissection avec trapèze >>> Aires dans la figure à trois carrés >>>	Aires des parallélogrammes >>> Hexagone >>> Avec deux carrés >>> Avec double triangles >>> Avec trois triangles (Einstein) >>> Avec des triangles quelconques >>> En trois dimensions (tétraèdre) >>>
Démonstrations par similitudes / proportions	Triangles rectangles proportionnels >>> Identique, avec similitudes >>> Aires proportionnelles >>> Avec un rectangle inscrit >>>	Moyenne proportionnelle de Colburn >>> Cercle et proportions >>> Michael Hardy >>>
Démonstrations par l'algèbre	Pythagore et distance >>> Loi des sinus >>> Loi des cosinus (réciproque) >>> Vecteurs (somme) >>> Vecteurs (double triangle) >>> Produit vectoriel >>>	Avec les dérivées >>> Avec trigonométrie >>> Avec exponentielles >>> Avec les matrices >>> Hypoténuse (méthode tamoule) >>>
Démonstrations visuelles	Découpage pivotant d'Airy >>>	Sabliers (eau) >>>
Démonstrations par généralisation	Pythagore: cas particulier du théorème de Ptolémée >>>
Divers avec Pythagore et son théorème	Pythagore pour toutes les formes >>> Sur une droite (triple quad) >>> Trigonométrie rationnelle >>> Pappus-Clairaut >>> Trois carrés et quatre triangles >>>	Lunule >>> Pyramide >>> Carrés magiques de Pythagore >>> Heptagone de Pythagore >>>

Merci !

Merci à tous les contributeurs qui ont décrit ces démonstrations avant moi. Parmi eux: Patrice Debart (en français) et Alexander Bogomolny (en anglais) et autres.

Généralisation du théorème de Pythagore

Théorème de Pythagore Base: triangle rectangle Aire du grand carré = somme des aires des petits carrés c² = a² + b²
Base: triangle quelconque Généralisation à tout type de triangle. Théorème d'Al Kashi	Base: triangle rectangle Généralisation à toutes les formes proportionnelles aux longueurs des côtés. Le théorème du pitre à bord !

Voir Généralisation à trois dimensions (tétraèdre) / Brève 54-1075

Voir Généralisation à l'hyper-espace (matrices)

Curiosités avec Pythagore

haut

Brique de Pythagore

3² + 4² =	5²
5² + 12² =	13²

Triangles de même périmètre = 120

30, 40, 50 C'est le plus

24, 45, 51 petit trio.

20, 48, 52 ayant cette propriété

Deux triangles de même aire = 24

Voir Brique de Pythagore / Pavé

Devinette – Solution

Question

Un lanceur de javelot voyage avec son engin de 2,40 m de long. Comment s'y prend-t-il pour prendre l'avion, sachant que l'aéroport n'accepte aucun colis de plus de 2,20 m de long?

Solution

Il confectionne une boite pour placer son javelot en travers. Alors, la largeur de la boite doit légèrement dépasser:

Retour / Informations complémentaires

Retour	Théorème de Pythagore – Débutants Pythagore pour toute figure (outre le triangle)
Suite	Application du théorème pour débutant Autres démonstrations originales Démonstration muette par dissection Démonstration de l'inverse du théorème de Pythagore Autres pages en en-tête ou en nomenclature des types de démonstrations
Applications du théorème	Application au calcul du trajet des fourmis sur pavé ou sur cylindre Approximation de Pi avec les triplets Calcul de la longueur de l'hypoténuse façon tamoule Démonstration de la formule de Héron Dissection de Dudeney Exemples de calculs Football – Temps de réaction du gardien Invariant de la relativité (Minkowski) Le théorème en 3D – Cas de la pyramide Les 17 équations qui ont changé le monde Propriétés des trois triangles Toutes les relations dans le triangle quelconque Heptagone de Pythagore
Voir	Addition – Glossaire Années Pythagore Bi, tripartitions Bouleversements et crises en maths Carré somme de cubes Cercle Conjecture de Riemann Conjecture d'Euler Décade de Pythagore Nombre = sommes de puissances Nombres carrés Nombres polygones	Nombres triangles Partitions Petit théorème de Fermat Pythagore – Biographie Somme de puissances Somme multi puissantes Th de Fermat-Wiles Théorème de Thalès Théorie des nombres Toutes les relations dans le triangle quelconque Triangle Unité des puissances
Livre	The Pythagorean proposition – Elisha Scott Loomis – 1940 (2^e édition) – 310 pages. 370 démonstrations dont 109 algébriques (calculs), 255 géométriques (aires), 4 vectorielles et 2 mécaniques (dynamique).
Sites	Démonstrations géométriques de Pythagore – Descartes et les Mathématiques – Patrice Debart – Très complet La secte des nombres – 2019 – Claudi Alsina – CNRS Quelles démonstrations pour le théorème de Pythagore ? – Alain Bernard et Brigitte Roussel Théorème de Pythagore – Wikipédia Théorème de Pythagore : dissection de Perigal – Cordierphychi – Vidéo Encore une preuve du théorème de Pythagore – 2019 – André Navas – CNRS Démonstrations géométriques de Pythagore – Mathématiques Internet Aix Marseille Pythagorean Theorem – Cut-the_knot – Alexander Bogomolny – Revue (en anglais) de quantité de démonstrations Pythagorean Theorem – Alexander Bogomolny – 2005 – 54 démonstrations Many Proofs of Pythagorean Theorem - Takaya Iwamoto – 2006 – Animations The Pythagorean Theorem by Stephanie J. Morris A mathematical Fable – Numberphile Teorema di Pitagora – Animation avec geoGebra
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Addition/ThPythDe.htm

BIENVENUE en particulier

aux professeurs et élèves des écoles et lycées

En effet: cette page est liée à un site qui vous est dédié: NOE-éducation

Sur ce site, vous trouverez de nombreuses idées de travaux pratiques, de problèmes, devinettes et puzzles.

En fait, une panoplie d'informations qui visent à se familiariser avec les nombres par la pratique, et, cela, dans toutes les disciplines. Vous serez alors armés pour aller explorer les bases de la théorie des nombres.

Voir aussi:

Débutant ***Nouveautés

Index alphabétique Pages les plus visitées

Calcul mental Humour

Géométrie Jeux

Outils mathématiques Culture générale

Tables Sciences

---