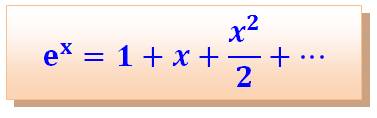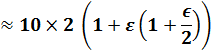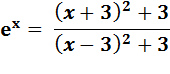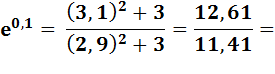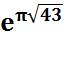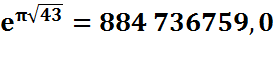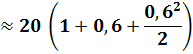NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 14/10/2014 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Analyse
Débutants Général	Développements			Glossaire Général
INDEX Puissance Décomposition Calcul mental	Fonctions	Dévelop. (1 + x)^a	Calcul exponentielles
	Terminale	Sommaire de cette page >>> Données connues >>> Calcul mental d'exponentiel 3 (Feynman) >>> Exponentiel x pour x petit (Padé)

Calcul des exponentielles

en utilisant les développements limités

Célèbre méthode de calcul mental de Feynman

Donnée supposées connues
Ces valeurs sont connues de Feynman du fait de ses travaux habituels.

Calcul mental de e^3 (méthode Feynman)
ln 10 + ln 2 =	2,995732274 = 3 – 0,004267726…	Propriété de cette somme de log >>>
=		Utilisation du développement e^x = 1 + x+ x² / 2
		e^3 = 20,0855369…
=	= e^3 x e = 20,0855369… x 2,71828182… = 54,598149800 …	e^4 =54, 598150033…

Voir Calcul d' exp (Pi racine de 163)

Remarque

Feynman aurait donné la valeur 20, 085. Ce qui est déjà un exploit!

Exponentiel x pour x petit
Approximation de Padé (l'une d'elle) Pour < 1/2
Exemple avec x = 0,1	= 1,105 170 902 … pour: 1,105 170 918 …

Henri Padé (1863-1853) mathématicien français

Cas de 43
		Il était connu que la valeur valait presque 20.
	= e^20,600.. (20,085)^6 x (1,718)^2 = 65 649 438,… x 2,9515… = 193 765 893, …

Suite	Développements limités
Voir	Développements finis Exponentielles Racine Racine carrée
Cette page	http://villemin.gerard.free.fr/aMaths/Analyse/Develop/CalExpo.htm