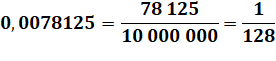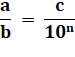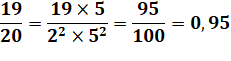NOMBRES - Curiosités, théorie et usages

 

Accueil                           DicoNombre            Rubriques           Nouveautés      Édition du: 16/06/2017

Orientation générale        DicoMot Math          Atlas                   Références                     M'écrire

Barre de recherche          DicoCulture              Index alphabétique                               

     

Nombres

 

Débutants

Fractions

NOMBRES PÉRIODIQUES

 

Glossaire

Fractions

 

INDEX

 

Fractions

 

Représentation des nombres

 

Débutants

Tour d'horizon

Longueur de la période

Nombres décimaux

Nombres périodiques

Dichotomie de la période

Premiers longs

Nombres cycliques

Extraction des décimales

Fractions en 1/99…99

142 857

Égalité 0,999 = 1

Cas particuliers

 

Sommaire de cette page

>>> Nombres décimaux

>>> Exprimer une fraction en nombre décimal

>>> Convertir un nombre décimal en fraction

>>> Fractions et nombres décimaux

>>> Théorème des nombres décimaux

>>> Table avec les puissances de 2 et de 5

 

 

 

 

 

 

Nombres DÉCIMAUX

FRACTIONS à développement fini

 

Les nombres avec des décimales sont tous les nombres comportant une virgule, comme: 3,14…

Mais, les nombres décimaux sont les nombres avec une quantité limitée de décimales, comme: 0,125.

Voir Cartographie des nombres périodiques

Anglais: regular numbers

 

 

Nombres décimaux

 

Le nom de nombres décimaux est réservé aux nombres totalement connus; aux nombres ayant une quantité finie de décimales.

 

Note: Ils sont parfois inclus dans la définition des nombres périodiques ave une période égale à 0.

 

Un nombre réel est un nombre décimal si et seulement si son développement décimal n'est constitué que de zéros à partir d'un certain rang.

 

 

Propriété

Ce sont les nombres issus d'une fraction ayant pour dénominateur un nombre d = 2a. 5b.

 

Soit: d = ( 2, 4, 5, 8 10, 16, …)   >>>

 

En représentation

Un nombre décimal possède plusieurs représentations:

0,5 = 0, 5000… = 0,4999…

 

On peut toujours remplacer les 0 terminaux par des 9, tout en décrémentant d'une unité le dernier chiffre significatif.

 

 

 

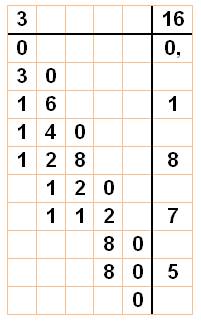
Exprimer une fraction en nombre décimal

Il suffit d'effectuer la division du numérateur par le dénominateur.

 

Par exemple: 3/16 = 0,1875 

 

Convertir un nombre décimal en fraction

 

Former une fraction avec un dénominateur en puissances de 10; autant de 0 que de chiffres après la virgule.

Simplifier la fraction en divisant par le même nombre en haut et en bas.

 

 

 

 

 

 

Fractions et nombres décimaux

 

Une fraction irréductible est convertie en nombre décimal si et seulement si son dénominateur ne contient aucun facteur premier autres que 2 et 5.

 

Supposons une fraction irréductible et sa conversion en décimal.

En multipliant par 10n

Le nombre c étant entier, b divise a x 10n

Or,  a et b sont premiers entre eux (fractions irréductible).

10n est divisible par b

Tous les facteurs de b doivent êtres dans 10n

Donc, que des 2 ou des 5.

b = 2k x 5h

Est-ce suffisant? Prenons, comme exemple:

Multiplions par 5 pour égaliser les exposants au dénominateur.

Il est toujours possible de procéder à cette opération.

Voir Division décimale

 

 

 

Théorème des nombres décimaux

 

 

Toutes les fractions en 1 / (2x . 5y)

ont un développement décimal fini.

 

La démonstration est relativement simple et rapide.

 

 

*    Soit donc notre fraction.

 

*    Multiplions en haut en bas par le même nombre.

*    Une seule fraction: le produit de deux fractions est égal au produit des numérateurs divisé par le produit des dénominateurs.

*    En regroupant puissance de 2 et puissance de 5: les exposants s'ajoutent.

*      Avec le même exposant, les deux nombres se multiplient.
 

 

 

 

 

 

 

 

Exemples

 

 

 

 

 

Table

Puissances de 2 et de 5 jusqu'à N = 1000

 

Les observations sur les premières fractions nous amènent à établir le tableau suivant:

 

x

y

M = 2x . 5y

N = 1/N

0

0

1

1

1

0

2

0, 5

2

0

4

0, 25

0

1

5

0, 2

3

0

8

0, 125

1

1

10

0, 1

4

0

16

0, 0625

2

1

20

0, 05

0

2

25

0, 04

5

0

32

0, 03125

3

1

40

0, 025

1

2

50

0, 02

6

0

64

0, 015625

4

1

80

0, 0125

2

2

100

0, 01

0

3

125

0, 008

7

0

128

0, 0078125

5

1

160

0, 00625

3

2

200

0, 005

1

3

250

0, 004

8

0

256

0, 00390625

6

1

320

0, 003125

4

2

400

0, 0025

2

3

500

0, 002

9

0

512

0, 001953125

0

4

625

0, 0016

7

1

640

0, 0015625

5

2

800

0, 00125

3

3

1000

0, 001

 

 

 

 

 

 

 

Retour

*    Nombres périodiques – Tour d'horizon

Suite

*    Nombres périodiques

Voir

*    Calcul mental – Index

*    Clé de divisibilité

*    Conversion des nombres en base b – Programme

*    Développements limités

*    Fractions continues

*    Fractions de Farey

*    Géométrie – Index

*    Nombre 0,1347…

*    Nombre magique 142857

*    Nombres décimaux

*    Nombres rationnels

*    Nombres têtus

*    Théorie des nombres – Index

Site

*    Regular number – Wolfram MathWorld

Cette page

http://villemin.gerard.free.fr/Wwwgvmm/Nombre/aaaCycli/DevLimit.htm