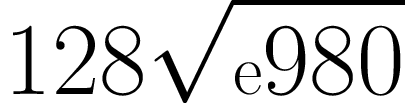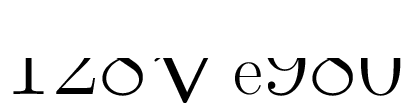|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
RACINES
|
Voir Radical
Message
caché avec racine: I LOVE YOU
|
Quelle est la
valeur de cette formule? Pas besoin de calculer! Elle renferme un
message secret visant la personne aimée. Il suffit de lire
la moitié inférieure de la formule: I love you (je t'aime).
À titre indicatif,
le calcul donne: 128 x 14 x |
Calculateurs
prodiges
|
Racine treizième d'un
nombre de cent
chiffres:
|
Voir
Pensées & humour
|
|
|||
|
Notation |
n 2 4 |
Le
symbole Évolution
à partir de la lettre r. Du
latin radix (racine). Introduit par Christoph
Rudolff 1525. |
|
|
|
Notation
fractionnaire n Notation sans exposant n |
||
|
Usage |
La racine deuxième est
appelée racine carrée: 2 La racine troisième est
appelée racine cubique 3 |
||
|
Définition |
La racine nième de a est
un nombre r tel que rn =
a Alors, on note
r = n |
||
|
Maths |
L’ est une bijection
de dont l’inverse est noté: |
|
|
|
Propriétés |
Tout nombre complexe z admet n racines nièmes complexes. Tout nombre réel
x |
||
|
L'élève:
les racines des mots sont-elles carrées? Le
professeur: carrées ou cubiques. C'est selon. Eugène Ionesco, La Leçon |
Voir Pensées & humour
|
|
|||
|
Ce qu'il faut savoir |
Une
racine est une puissance avec l'inverse de l'exposant:
|
||
|
Méthode |
La
procédure semble un peu longue, car décrite pas à pas. On
montre d'abord comment accéder à la calculette de l'ordinateur; Puis
le calcul d'une puissance avec la touche xy; et Enfin,
le calcul d'une racine (n) via la puissance inversée (1/n). |
||
|
Accès à la calculette scientifique de l'ordinateur. |
1.
Cliquer en bas de l'écran à gauche (image =>) 2.
Tous les programmes 3.
Dossier : Accessoires |
|
|
|
4.
Sélectionner Calculatrice |
|
||
|
5.
Affichage: choisir
Scientifique |
|
||
|
Calcul d'une puissance 210 = 1024 |
1.
Introduire le nombre (2) sur la calculette ou sur le clavier numérique
de votre ordinateur |
|
|
|
2.
Sélectionner la touche xy |
|
||
|
3.
Introduire l'exposant (10) |
|
||
|
4.
Faire = sur la calculette ou Entrée sur le clavier |
|
||
|
Calcul d'une racine
Même méthode que pour la
puissance. Cependant, il faut mettre la fraction 1/19 entre parenthèses pour
qu'elle soit calculée en premier lieu. Puis, on exécute l'élévation à la
puissance. |
1.
Introduire le nombre 2 |
|
|
|
2.
Sélectionner la touche xy |
|
||
|
3.
Ouvrir la parenthèse (touche parenthèse) |
|
||
|
4.
Taper 1/19 |
|
||
|
5.
Fermer la parenthèse (la valeur affichée est égale à 1/19) |
|
||
|
6.
Appuyer sur = ou Entrée |
|
||
Voir Table
des racines énièmes de 2
|
|
||
|
Avec la conclusion que surd est l'instruction à utiliser! Voir aussi Racine carrée |
||
|
Calcul
avec fraction
|
La racine cubique
de 8 est bien 2 (2.0000… en virgule
flottante). L'opposée de la
racine cubique de 8 est bien l'opposée de 2, soit - 2. Jusque là tout va bien
Mais, voyons le
dernier exemple qui est celui qui peut se produire lors d'un calcul
algébrique. La valeur donnée
pour la racine cubique du nombre –8 est un nombre complexe. C'est une des
racines mais il en manque deux. |
|
|
Calcul
avec l'instruction root (racine) |
L'instruction
root permet de calculer la racine énième d'un nombre. Avec un nombre
positif, la valeur est celle attendue. Avec un nombre
négatif, le résultat donné en mentionnant la racine cubique (1/3) de –1. L'évaluation
flottante redonne le même résultat qu'ave la méthode des fractions. |
|
|
Calcul
avec l'instruction surd (radical) |
Avec cette
instruction, nombre positif ou négatif, nous obtenons sa racine réelle. Voir application
à la résolution de l'équation du troisième
degré |
|
|
Cette illustration
montre le domaine de définition de la puissance fractionnaire (rouge) et de
celui de l'instruction surd (vert). Explication
du programme Plot est
l'instruction de dessin de graphe. Les crochets
permettent de définir deux fonctions à dessiner sur le même graphe. La dynamique en
abscisse est définie par x = de -2 à + 2. |
||
|
Quel
est le nombre N tel que sa racine carrée et celle du nombre précédent est
inférieure à 1/100?
L'idée
consiste à inverser l'égalité:
En
multipliant par le conjugué pour éliminer les racines au dénominateur:
Ces
deux nombre sont proches:
N > 2 500 La
plus petite valeur de N pour une différence:
|
N et écart de sa racine avec la précédente Centième Millième Dix
millième |
Voir Identités
avec racines / Nombre
2500
|
Solution immédiate (avec intuition de que 2 + 1 =
3)
Solution algébrique
Division du polynôme – Explication Autres
racines Le polynôme en a4
a quatre racines: deux réelles et deux imaginaires. La seconde
réelle conduit à: x = 14,9656685004… (résolution de l'équation en a3). |
Voir Division des
polynômes / Brève
726




|
Notation:
a + b = 1 |
Calcul Voir Nombre
d'or |
|
|
Démonstration Notez l'utilisation de l'identité
(a + b) (a – b) = a² - b² sous la racine cubique.
Cette
expression prend également deux valeurs complexes en optant pour les deux
autres racines cubiques complexes de -1:
1,927050983… + 0,5352331342 i Notes: nous
venons de voir que:
Exploration d'autres cas
|
||
Voir Calcul des racines
Quelques exemples de calculs avec des puissances fractionnaires
avec
2^(5/2) et 2^(3/2)

|
|
||||||
|
Words |
|
|||||
|
Definition |
Squ The
squ For
example, nth root The
nth root of For
example, a fourth root of 16 is R The
word r |
|||||
![]()
|
Suite |
|
|
C |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()