NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 28/05/2014 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Dénombrement
Débutants Général	Principe des TIROIRS			Glossaire Général
INDEX Dénombrement	Débutant	Exemples	Connaissances	Nb en 00 ..01
	Introduction	Divisibilité 10	Divisibilité 2n	Divisibilité n
		Sommaire de cette page >>> Propriété >>> Démonstration >>> Expérimentation

n nombres divisibles par n

Propriétés fascinantes de divisibilité d'une sélection quelconque de n nombres.

PROPRIÉTÉ
Données On choisit n entiers, distincts ou non. Affirmation 1 Il existe toujours un sous-ensemble de ces entiers dont la somme est divisible par n. Affirmation 2 Dans la liste ordonnée de ces nombres, il existe deux rangs p et q tels que la somme des nombres entre ces deux rangs est divisible par n.	Exemples n = 4 1, 13, 7, 5 1 + 7 = 8 divisible par 4 1, 5, 7, 13 7 + 13 = 20 divisible par 4 5 + 7 = 12 divisible par 4

Démonstration
Principe Démonstration en deux temps On va trouver deux nombres qui produisent le même reste dans la division par n et, Dire que leur différence est divisible par n.
Démonstration Formons les sommes suivantes:	s1 = a1 , s2 = a1 + a2 , … , sn = a1 + a2 + … + an
Il se peut qu'une des sommes soit divisible par n, alors on aurait trouvé ce que l'on cherche.	Dans le cas où une somme est divisible par n, le reste est 0. Dans les autres cas, le reste sera différent de 0.
Sinon, on considère leur reste dans la division par n (on dit modulo n).	Il y a n sommes. et n – 1 restes possibles (car le 0 est exclu, comme vu ci-dessus).
Selon le principe des tiroirs, il y toujours deux restes identiques	sp = sq
La différence de ces deux nombres est la somme des nombres initiaux des rangs q+1 à p (en supposant que Sp est le plus grand).	sp = a1 + a2 + … + aq + aq+1 + … + ap sq = a1 + a2 + … + aq sp – sq = aq+1 + … + ap
Leur différence, qui est une certaine somme des nombres initiaux, est divisible par n	sp – sq est divisible par n ou autrement dit: sq – sq = 0 mod n

Expérimentation

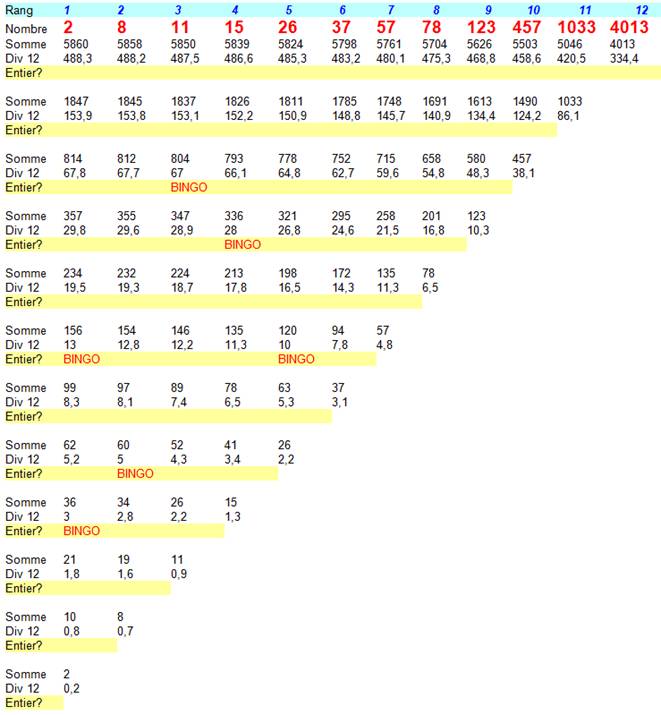
Principe et explication du tableau Nous allons vérifier l'affirmation 2. Prenons 12 nombres (n = 12) au hasard, ordonnés du plus petit au plus grand (rouge) La ligne "Somme" est le cumul de la somme du plus grand vers le plus petit (Ex: 5046 = 4013 + 1033). La ligne "Div 12" est la division de ce cumul par 12; le résultat est entier ou décimal La ligne "Entier" est marquée BINGO dès qu'un de ces cumuls est divisible par 12 Tableau des nombres et des calculs Observations Le premier cumul divisible par 12 est 804, somme des nombres des rangs 3 à 10. Un deuxième apparaît 336 comme la somme des nombres des rangs 4 à 9. Au total, nous avons six sommes divisible par 12, plus qu'il n'en faut pour vérifier notre affirmation.

Suite	Dénombrement et tiroirs Divisibilité Paires divisibles
Voir	Coïncidences Dénombrement et tiroirs Sudoku Exemples d'applications
Aussi	Compter Jeux – Index
Cette page	http://villemin.gerard.free.fr/aMaths/Denombre/Tiroir/TiroirSo.htm