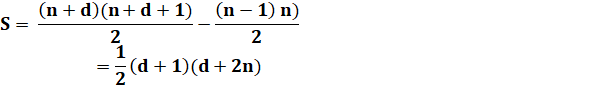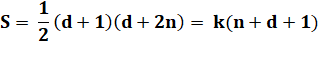|
|||||||||||||||||||||||||||||
![]()
|
Somme
de nombres consécutifs On connaît la somme 1 + 2 + 3 + 4 = 5 x
2 = 10, égale au double du nombre qui suit. Quelles sont les configurations
de ce type? Pas si répandues que cela! Par exemple: 3 + 4 + 5 = 6 x 2 = 12 En bref, nous cherchons donc des sommes de nombres consécutifs avec
deux nombres successifs de part et d'autre du signe égal. |
|
|
|
|
|
|
|
|
|
|
|
|
|
= k (les r suivants) |
|
|
|
|
|
= k fois le précédant |
|
|
Exemple: 5 + 4 = 3 x
3 = 9
Coquetterie pour les deux dernières sommes: elles finissent par
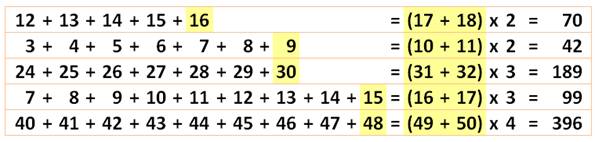
l'inversé du nombre de départ. Pour quelques unes, la somme des nombres symétriques permet de
calculer la somme totale et donne immédiatement le facteur multiplicatif.
Comme pour 3 + 4 + 5 + 6 = (3 + 6) + (4 + 5) = 2 x 9 . |
|
|
|
|
|
|
|
|
Nous avons trouvé
quelques belles et rares configurations durant notre balade dans le paysage
si varié des nombres. Retenons: 1 + 2 + 3 + 4 = 5 x 2 3 + 4 + 5 = 6 x 2 6 + 7 + 8 + 9 = 10 x 3 3 + 4 + 5 + 6 + 7
+ 8 + 9 = (10 + 11) x 3 5 + 4 = 3 x 3 9 + 8 + 7 = 6 x 4 9 + 8 + 7 + 6 = 5 x 6 |
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/MOTIF/Operatio/Somme.htm
|
![]()