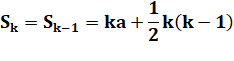|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Énigmes des cinq pots & Sommes de consécutifs Comment partager les billes
dans cinq pots selon certaines conditions? Quel est le minimum de billes? Une énigme qui conduit à une
propriété sur les sommes de nombres consécutifs. Exemple
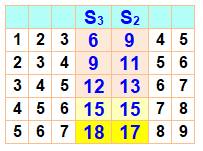
En commençant par 5 billes ou plus, la balance penchera vers la gauche
et cela même en échangeant des nombres d'un plateau à l'autre. Comparez les
écarts entre quantité de billes vertes et de billes violettes. Voir tout de suite la
propriété >>> |
|
|
|
|
Énigme Cinq pots dans lesquels on place des billes:
Solution On pose a, b, c, d et e les quantités de billes. Ces valeurs sont différentes: a < b < c < d < e Chaque pot successif contient au moins une bille de plus que le
précédent: d > c > b e > d > c d Les trois premiers pots contiennent plus que les deux derniers: a + b + c > d + e a + b + c > b + 2 +
c + 2 a > 4 Testons les plus petites valeurs avec a = 5 5, 6, 7, 8 et 9 Total 35 Total des trois premiers 18 Total des deux derniers 17 Total des autres configurations toujours satisfait car le cas examiné
était le cas avec les valeurs les plus faibles pour la somme de trois. Toute
autre somme donnera un total plus grand et une somme des deux autres plus
petite Ex: 5 + 6 + 8 = 19 > 7 + 9 =
16 |
|
|
|
||
|
Cette
énigme révèle une propriété des nombres. Avec cinq nombres consécutifs à partir de 5,
toute somme de trois d'entre eux est supérieure à la somme des deux autres. Pourquoi à partir de 5? Si le premier est a, le suivant est a +1, etc. La somme des trois plus petits est: Celle des deux plus grands est: Relation entre les deux: Le nombre a est positif Pourquoi toutes les permutations Le cas étudié est le cas le plus critique: en
échangeant deux nombres, c'est un plus grand qui entre dans le club des trois
et un plus petit dans celui des deux, renforçant l'inégalité. |
Exemple avec les premières valeurs
Toutes les permutations avec {5, 6,
7, 8, 9 }
|
|
|
|
|
|
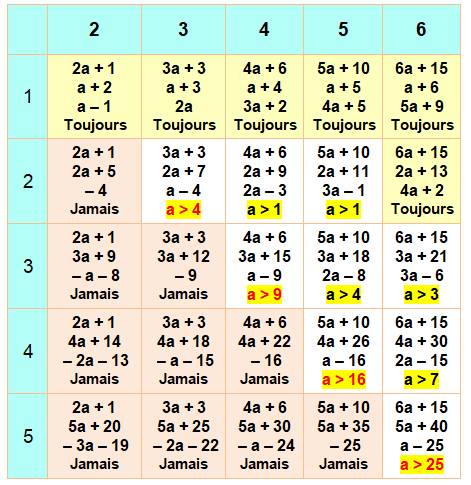
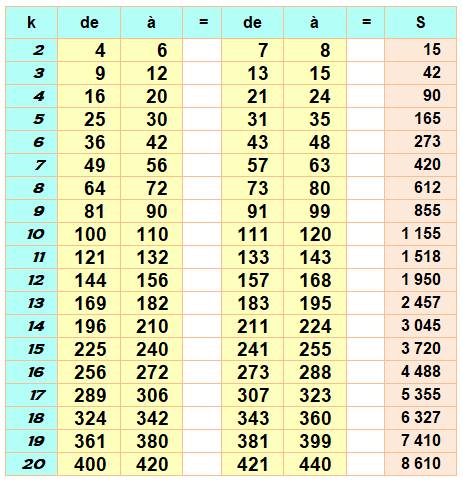
Lecture de la table L'exemple vu ci-dessus est noté S3S2 et se trouve
en colonne 3 et ligne 2, case dans laquelle on trouve: S3 = 3a + 3; S2 = 2a + 7; S3 – S2 = a – 4
qui conduit à la condition: S3 est plus grand que S2 pour a plus grand que 4.
Exemple complémentaire Avec S5S4, en colonne 5 et ligne 4, la conclusion
est que S5 > S4 si a > 16 En effet: 16 + 17 + 18 + 19 + 20 = 5 x 18 = 90 et 21 + 22 + 23 + 24 = 4 x
22, 5 = 90. Soit égalité; il faudra un de plus pour que S5 soit supérieur à
S4. |
|
Point de situation -
Propriété
|
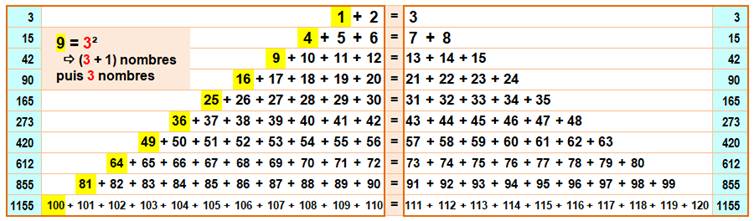
Propriété étonnante: égalité sans fin de sommes
d'entiers consécutifs
Notez que le nombre
en-tête est un carré; les carrés successifs. Pas si mystérieux !
L'indice
derrière le crochet indique la quantité de termes. Somme: k3
+ k² + k(k + 1) / 2; Pour k = 5: 125 + 25 + 5
× 3 = 165 En bleu,
la somme
des entiers de 1 à k. Théorème La somme de k + 1 nombres successifs à partir de k² est égale à la somme des k suivants. Exemple K = 10 100 + 101 + … + 110 = 111 + 112 + … + 120 = 1155 |
Voir Brève
48-956
|
Autre démonstration |
|
|
|
La démonstration ci-dessus consiste à prouve l'égalité
des sommes est juste. La démonstration ci-dessous consiste à chercher
la valeur de a,
le nombre initial de la somme de gauche, pour obtenir l'égalité. |
||
|
Formules pour Sk et de Sk-1 a est le nombre qui débute la somme de gauche. |
|
|
|
Valeur de a pour égalité |
|
|
|
Retour à l'inégalité |
Si la somme commence par un nombre plus grand que
k², alors la première somme est plus grande que la seconde, et, l'inégalité
reste vraie quelle que soit la permutation des 2k + 1 nombres. |
|
|
|
||
|
Plus simple! |
Sur l'exemple S4S3, prenons ce qui
"dépasse": 0 + 1+ 2 + 3 et 4 + 5 + 6. L'écart est de 15 – 6 = 9 Pour compenser cet écart, il faut ajouter k à
chaque nombre avec k tel que : 5k = 4k + 9, soit k = 9. Et donc, en ajoutant 9 partout: 9 + 10 + 11 + 12
= 13 + 14 + 15. |
|
|
Révélation! |
Voyons cela plus précisément. Comment passe-t-on des deux sommes de nombres
successifs à une égalité ?
|
|
|
|
|
|
Sweets in five jars in such a way that no jar is empty and no two jars
contain the same number of sweets. Also, any three jars contain more sweets in total than the total of
the remaining two jars. What is the smallest possible number of sweets altogether in the five
jars? |
|
Source: UK Junior
Mathematical Olympiad 2010
|
|
![]()
|
Voir |
|
|
Aussi |
|
|
DicoNombre |
|
|
Cette page |
![]()