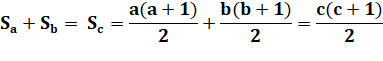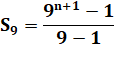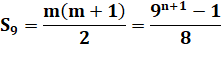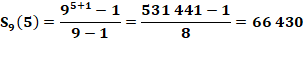|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
SOMME des ENTIERS avec nombres
consécutifs (2/2) Suite de la page sur la somme des entiers: quelques propriétés
et curiosités. Exemple:
la somme des entiers jusqu'au nombre 3 additionnée à la somme des entiers
jusqu'au nombre 5 est égale à la somme des entiers jusqu'au nombre 6. >>>
|
Étonnant ! – Sommes partielles d'entiers
|
Observations
Théorème La somme de k + 1 nombres successifs à partir de k² est égale à la somme des k suivants. |
Voir Suite
avec l'énigme des cinq pots / Brève
48-956
|
|
||
|
Théorème La somme des entiers successifs produit les nombres triangulaires. Sn = 1 + 2 + 3 + ... + n = n ( n + 1 ) / 2 = Tn Notez que parmi les deux nombres n et n + 1, l'un est pair et l'autre impair; le
produit est toujours divisible par 2. |
Valeurs Rang
Tn 0 0 1 1 2 3 3 6 4 10 5 15 6 21 7 28 8 36 9 45 10 55 100 5 050 1 000 501500 10 000 50015000 100 000 5000150000 n n
( n + 1 ) / 2 |
|
|
(somme des entiers
consécutifs) |
Exemple |
Formulation |
|
Prenons l'exemple: |
1 + 2 + 3 + 4 = 10 |
1
+ 2 + ... + n |
|
La moyenne de ces 4 nombres est: |
10 / 4 = 2,5 = ½ 5 |
½
(n + 1) |
|
Si on veut leur somme, on multiplie
par la quantité de nombres. |
4
x ½ 5 = 10 |
½
n (n + 1) |
|
Exemple |
Formulation |
|
|
Somme des entiers de m à n: |
4 + 5 + 6 = 15 m = 4 et n = 6 = 1/2 (6x7 – 3x4) = 30/2 = 15 |
|
|
Somme de n entiers consécutifs
supérieurs à n ou nombre pentagonaux
du deuxième ordre |
S = 6 + 7 + 8 + 9 + 10 = (3x5² + 5) / 2 = 40 |
|
Somme des entiers à k chiffres
|
Approche S(2) = 100 + 101 + … + 999 = 4 905 La somme des nombres à deux chiffres est égale à
4 905. C'est la somme de tous les nombres jusqu'à 999,
diminuée de la somme de ceux jusqu'à 99. Formule générique Si a = 10k et b =
a/10
Exemple k = 3: S(3) = 99 x 1003 / 200 – 9 x 103 / 20 =
495 000 – 450 = 494 550 Allure du nombre Tous ces nombres sont de la forme: 494 99…9k-3 55 00…0k-2
Exemple k = 10: S(10) =
494 9999999 55 00000000 Démonstration Il faut ajouter les nombres de 10k-1 à 10k – 1. Soit 10k – 1 – 10k-1 + 1 = (10 – 1) 10k-1 = 9 10k-1 termes. Il s'agit d'une progression
arithmétique:
Table des sommes des nombres à k
chiffres (k, S)
|
Voir Brève
800
|
|
||
|
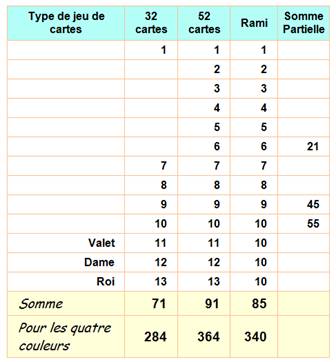
Application Compter le nombre de points dans un jeu de cartes. Note Au Rami comme pour le Black Jack, les figures comptent
pour 10 points. L'as compte pour 1 ou 11 points. Suite >>> |
|
|
|
|
||
|
Une application de la somme des entiers. Énigme En
faisant la somme des entiers de 1 à n avec n < 11, un enfant trouve 40. Visiblement,
il a oublié de compter un nombre. Lequel ? Réponse C'est le 5 qui manque |
Solution par recherche On dresse ce petit tableau
avec les sommes des entiers de 1 à n qui
se trouvent autour de 40:
Solution par équation Traduction sous forme d'équation: 40 = ½ n (n + 1) – x 80 = n (n
+ 1) – 2x 2x = n (n
+ 1) – 80 Il faut trouver deux nombres
consécutifs dont le produit est
supérieur à 80. Le premier de la sorte est 9 x 10 = 90 2x = 90 – 80 et x = 5 Il s'agit donc de la somme des nombres jusqu'à 9 sans le 5. Vérification ½ (9 x 10)
– 5 = 45 – 5 = 40 Essayons le produit
suivant: 10 x 11 2x = 110 – 80 et x = 15 15 est trop grand puisqu'il s'agit de la somme
des nombres de 1 à 10. |
|
|
Même énigme mais l'enfant à
oublié deux nombres. Impossible! |
Dans ce cas, pour faire 5,
il aurait oublié les couples: (1, 4) ou (2, 3). Et pour faire 15 avec un
total de 55, donc sans dépasser 10: (5, 10), (6, 9) ou (7, 8). Exemple:
1 + 2 + 3 + 4 + 5 La somme suivante est 66.
L'écart serait de 26, inatteignable avec des nombres inférieurs ou égaux à
11. |
|
Voir Énigme du nombre manquant connaissant la
moyenne / Énigmes – Index
Merci à Yann
pour sa relecture attentive
|
|
||
|
Que
penser de cette égalité? |
|
|
|
On
connait la formulation de la somme des
entiers. |
|
|
|
Après
développement et simplification. |
|
|
|
Existe-t-il
des solutions? OUI, par exemple: |
3² + 5² – 6² = 6 – 3 – 5 9 +
25 – 36 = -2 |
|
|
En effet,
on retrouve les sommes des entiers: |
1 + 2 + 3 = 6 1 + 2 + 3 + 4 + 5 = 15 1 + 2 + 3 + 4 + 5 + 6 = 21 |
|
|
Autres cas Première
solution (avec répétition). |
2² + 2² – 3² = 3 – 2 – 2 = –1 |
|
|
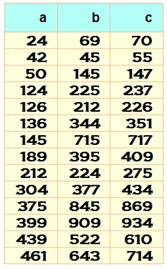
Il y a 15 solutions pour a,
b et c jusqu'à 25. Il y a 98 solutions pour a,
b et c jusqu'à 100, et 1 699 jusqu'à 1000. Exemple de lecture En
dernière ligne: S14
+ S18 = S23 = 1 + 2 + 3
+ … + 14 + 1 + 2 +
3 + … + 18 = 1 + 2 +
3 + … + 23 |
Note: les cas
(9, 13, 16) et (11, 20, 23) montrent que l'égalité est possible même
si les trois nombres sont premiers entre eux deux à deux. |
|
|
Cas de
quatre sommes |
|
|
|
Un
exemple des plus simples. |
|
|
|
Les 12
solutions pour a, b, d et d jusqu'à 10. |
|
|
|
|
||
|
Sur notre
lancée, que penser de cette égalité avec des carrés? |
|
|
|
On
connait la formulation de la somme
des carrés. |
|
|
|
Tous
calculs faits: |
|
|
|
Existe-t-il
des solutions? OUI |
|
|
|
Les 14
solutions pour a, b et c jusqu'à 1000 |
|
|
|
Cas de
quatre sommes |
|
|
Exemples => |
|
|
Il y a 56
cas pour a, b, c et d jusqu'à 100, comme => |
4, 5, 5, 7 4, 6, 10, 11 10, 10, 14, 17 43, 51, 85, 94 (le plus grand) |
![]()
|
|
||
|
k = 2 k = 3 |
n + (n+1) = 2n + 1
Nombre impair (n–1) + n + (n+1) = 3n
Nombre divisible
par 3 Etc. Trivial |
|
|
|
|||
|
So / k = 2 |
n + (n – 1) = 2n – 1 Trivial |
3 + 2 = 2x3 – 1 = 5 |
|
|
Dif / k = 2 |
n – (n – 1) = 1 Trivial |
3 – 2 = 1 |
|
|
So / k = 3 |
(n + 1) + n + (n – 1) = 3n |
4 + 3 + 2 = 3x3 = 9 |
|
|
n + (n – 1) + (n – 3) = 3n – 3 |
4 + 3 + 2 = 4x3 – 3 = 9 |
||
|
Dif / k = 3 |
(n + 1) + n – (n – 1) = n + 2 |
4 + 3 – 2 = 3 + 2 = 5 |
|
|
So / k = 4 |
(n + 1) + n + (n – 1) + (n – 2) = 4n – 2 |
5 + 4 + 3 + 2 = 4x4 – 2 = 14 |
|
|
n + (n – 1) + (n – 2) + (n – 3) = 4n – 6 |
5 + 4 + 3 + 2 = 4x5 – 6 = 14 |
||
|
Dif / k = 4 |
(n + 1) – n – (n – 1) + (n – 2) = 0 |
5 – 4 – 3 + 2 = 0 5 + 2 = 3 + 4 |
|
Voir Nombres consécutifs – Sommes
/ Produits
|
|
|||
|
La somme des puissances successives de 9 est un nombre triangulaire. |
|
||
|
Il s'agit
dune suite
géométrique de raison 9 |
|
||
|
Nombre triangulaire: somme des entiers
consécutifs de 1 à m. |
|
||
|
Deux
expressions pour S9. |
|
||
|
Puissance
de 9 mise sous la forme d'un carré. |
|
||
|
Calcul de
m (identité
remarquable) |
|
||
|
En
fonction de m |
|
||
|
Valeur de
m |
|
||
|
Exemple: n = 5 |
|
||
|
Vérification |
|
||
Voir Brève
431 pour d'autres propriétés de cette somme
![]()
|
Retour |
|
|
Suite |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Identite/SomEntie.htm |
![]()