|
Édition du: 29/01/2020 |
|
INDEX |
PUISSANCES de 2 |
||
|
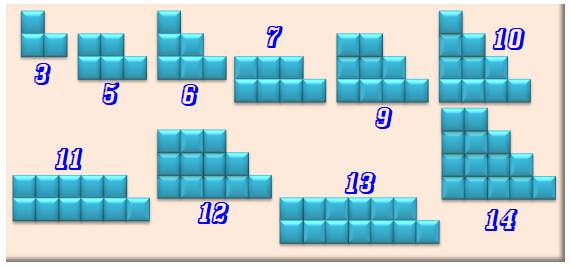
NOMBRES ESCALIERS Nombres POLIS ou nombres
trapézoïdaux
Nombres qui
peuvent s'écrire comme la somme de nombres consécutifs. Ces nombres
semblent simples et pourtant ils intéressent les experts de la théorie des
nombres. |
||
|
|
Sommaire de cette page >>> Définition >>> Propriétés >>> Liste |
Débutants Glossaire |
|
Un nombre poli ou escalier est un nombre qui peut s'écrire sous la
forme de une ou plusieurs sommes de deux ou plusieurs nombres consécutifs. Exemple: 15 = 1 + 2 + 3
+ 4 + 5 = 4 + 5 + 6 = 7 + 8 |
|
|
|
Tous les nombres peuvent se mettent sous la forme
de somme de consécutifs sauf les puissances de 2. Le degré de politesse indique combine de fois un
nombre est sommes de nombres consécutifs. |
Avec les nombres triangulaires Les nombres polis dont la somme commence par 1
sont les nombres
triangulaires. Tous les nombres polis sont différences de deux
nombres triangulaires: l'un qui va de 1 jusqu'au dernier nombre de la somme
et l'autre qui efface les nombres de 1 jusqu'au nombre avant celui qui
commence la somme. |
|
|
3, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 17, 18,
19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 33, 34, 35, 36, 37, 38,
39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57,
58, 59, 60, 61, 62, 63, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77,
78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96,
97, 98, 99, 100 |
Les nombres polis sont tous les nombres sauf les
puissances de 2. Notez que le 1 ne fait pas partie de cette
catégorie. Rappel des puissances de 2
2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096,
8192, 16384, 32768, 65536, 131072, 262144, 524288, 1048576 |
|
Voir Suite sur les
nombres polis
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/TYPDENOM/Escalier.htm
|
