|
|||||||||||||||||||||||||||||
![]()
|
NOMBRES POLIS et MULTISOMME de CONSÉCUTIFS Partition en nombres consécutifs Pratiquement
tous les nombres, sauf les puissances
de 2, sont somme de deux nombres consécutifs. Ils
sont même souvent sommes plusieurs fois de k nombres consécutifs. Les
nombres polis sont sommes non
triviales de nombres consécutifs. Ils sont très nombreux. Ceux qui ne le sont
pas sont les nombres impolis. Ceux qui le sont k fois sont k-polis. Tous les
nombres impairs (donc tous les nombres premiers, sauf 2) sont la somme de
deux nombres consécutifs. Ils sont tous polis. Exemple: le nombre 2019 est
3-polis, somme trois fois de nombres consécutifs:
Un autre exemple: Le
nombre 2025 est
14-poli. |
Voir Introduction en nombres
polis
Voir
Nombres par leur petit nom / Partitions
– Index
|
|
|||
|
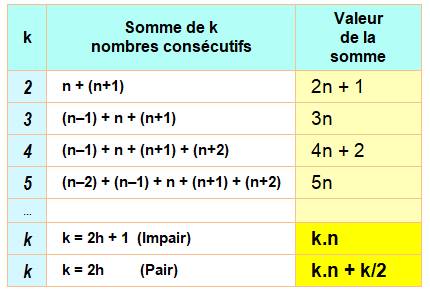
Établissement des règles En prenant
un nombre n comme élément central, on calcule la somme de k nombres
consécutifs autour de lui. |
|
||
|
Si k est
impair, la somme est un multiple de k. Si un nombre n est divisible par k, il est somme de k nombres
consécutifs*. Exemple: 15 = 3 x 5 = 4 + 5 + 6 15 = 3
x 5 = 1 + 2 + 3 + 4 + 5 * à condition que les termes de la somme soient positifs. |
Si k est
pair, la somme est un multiple de k plus la moitié de k. Si un nombre n diminué de k/2 est divisible par k, il est somme de k
nombres consécutifs*. Exemple: 45 – 6/2 = 42 = 6 x 7 Soit six nombres autour de 7 45 = 5 + 6 + 7 + 8 + 9 + 10 |
||
Merci à Stephan Schumacher pour sa relecture
attentive
|
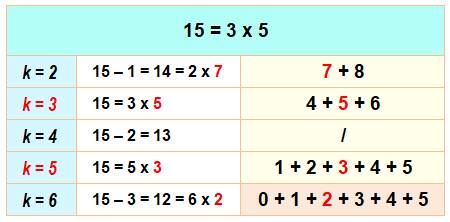
Exemples complets Le nombre 15 est trois
fois sommes de nombres consécutifs. Deux fois du fait de ces deux facteurs 3 et 5, et Une fois avec k = 2, ce qui toujours le cas pour
un nombre impair comme 15. Avec k = 6, on retrouve la somme précédente avec un 0 en plus. |
|
|
|
Le nombre 21 est trois
fois somme de nombres consécutifs. Diviseurs de 21: Ils sont quatre un
de plus que la quantité de sommes. |
|
|
|
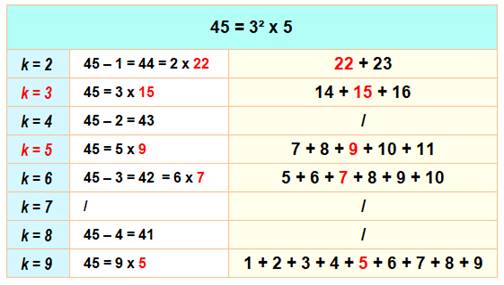
Le nombre 45 est cinq
fois somme de nombres consécutifs. Diviseurs de 45: Ils sont six, un
de plus de la quantité de sommes. |
|
|
|
|
||
|
La quantité de k-sommes d'un nombre n est égale à sa quantité de diviseurs impairs moins 1. |
Exemples Div(15) = 1, 3, 5, 15 => 3 sommes Div(45) = 1, 3, 5, 9, 15, 45 => 5 sommes Div(100) = 1, 2, 4, 5, 10, 20, 25, 50, 100
=> 2 sommes 100 = 18 + 19 + 20 + 21 + 22 = 9 + 10 + 11 + 12 + 13
+ 14 + 15 + 16 |
|
|
Div(2019) = 1, 3, 673, 2019 => 3 sommes 2019 = 1009 + 1010 = 672 + 673 + 674 = 334 + 335 + 336 +
337 + 338 + 339 |
Div(1000) = 1, 2, 4, 5, 8, 10, 20,
25, 40, 50, 100, 125, 200, 250,
500, 1000 = 3 sommes 1000 = 198 + 199 + 200 + 201 + 202 = 55 + 56 + … + 62 +… + 70 = 28 + 29 + … + 40 + … + 52 |
|
Merci à Jean B. pour
sa relecture attentive
|
|
||||
|
Polis (nombres pairs en rouge) 3, 5, 6, 7, 9, 10,
11, 12, 13, 14,
15, 17, 18, 19, 20,
21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, … |
Impolis 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, 16384,
… Ce sont les puissances
de 2. |
|||
|
Les premières valeurs explicitées jusqu'à 50 [nombre n, quantité de sommes,[nombre central, quantité de termes],
[idem]] Exemple: [9, 2,
[4, 2], [3, 3]]
=> 9 est somme 2 fois: 9 = 4 + 5 = 2 + 3 + 4 |
||||
|
[1, 0] [2, 0] [3, 1, [1, 2]] [4, 0] [5, 1, [2, 2]] [6, 1, [2, 3]] [7, 1, [3, 2]] [8, 0] [9, 2, [4, 2], [3, 3]] [10, 1, [2, 4]] [11, 1, [5, 2]] [12, 1, [4, 3]] [13, 1, [6, 2]] [14, 1, [3, 4]] [15, 3, [7, 2], [5, 3], [3, 5]] [16, 0] [17, 1, [8, 2]] |
[18, 2, [6, 3], [4, 4]] [19, 1, [9, 2]] [20, 1, [4, 5]] [21, 3, [10, 2], [7, 3], [3, 6]] [22, 1, [5, 4]] [23, 1, [11, 2]] [24, 1, [8, 3]] [25, 2, [12, 2], [5, 5]] [26, 1, [6, 4]] [27, 3, [13, 2], [9, 3], [4, 6]] [28, 1, [4, 7]] [29, 1, [14, 2]] [30, 3, [10, 3], [7, 4], [6, 5]] [31, 1, [15, 2]] [32, 0] [33, 3, [16, 2], [11, 3], [5, 6]] [34, 1, [8, 4]] |
[35, 3, [17, 2], [7, 5], [5, 7]] [36, 2, [12, 3], [4, 8]] [37, 1, [18, 2]] [38, 1, [9, 4]] [39, 3, [19, 2], [13, 3], [6, 6]] [40, 1, [8, 5]] [41, 1, [20, 2]] [42, 3, [14, 3], [10, 4], [6, 7]] [43, 1, [21, 2]] [44, 1, [5, 8]] [45, 5, [22, 2], [15, 3], [9, 5], [7, 6], [5, 9]] [46, 1, [11, 4]] [47, 1, [23, 2]] [48, 1, [16, 3]] [49, 2, [24, 2], [7, 7]] [50, 2, [12, 4], [10, 5]] |
||
Voir
Table
similaire
|
K-Polis |
|
|
|
Deux sommes jusqu'à 1000 [9, 2, [4, 2], [3, 3]] [18, 2, [6, 3], [4, 4]] [25, 2, [12, 2], [5, 5]] [36, 2, [12, 3], [4, 8]] [49, 2, [24, 2], [7, 7]] [50, 2, [12, 4], [10, 5]] [72, 2, [24, 3], [8, 9]] [98, 2, [24, 4], [14, 7]] [100, 2, [20, 5], [12, 8]] [121, 2, [60, 2], [11, 11]] [144, 2, [48, 3], [16, 9]] [169, 2, [84, 2], [13, 13]] [196, 2, [28, 7], [24, 8]] [200, 2, [40, 5], [12, 16]] [242, 2, [60, 4], [22, 11]] [288, 2, [96, 3], [32, 9]] [289, 2, [144, 2], [17, 17]] [338, 2, [84, 4], [26, 13]] [361, 2, [180, 2], [19, 19]] [392, 2, [56, 7], [24, 16]] [400, 2, [80, 5], [16, 25]] [484, 2, [60, 8], [44, 11]] [529, 2, [264, 2], [23, 23]] [576, 2, [192, 3], [64, 9]] [578, 2, [144, 4], [34, 17]] [676, 2, [84, 8], [52, 13]] [722, 2, [180, 4], [38, 19]] [784, 2, [112, 7], [24, 32]] [800, 2, [160, 5], [32, 25]] [841, 2, [420, 2], [29, 29]] [961, 2, [480, 2], [31, 31]] [968, 2, [88, 11], [60, 16]] |
Trois sommes jusqu'à 100 [15, 3, [7, 2], [5, 3], [3, 5]] [21, 3, [10, 2], [7, 3], [3, 6]] [27, 3, [13, 2], [9, 3], [4, 6]] [30, 3, [10, 3], [7, 4], [6, 5]] [33, 3, [16, 2], [11, 3], [5, 6]] [35, 3, [17, 2], [7, 5], [5, 7]] [39, 3, [19, 2], [13, 3], [6, 6]] [42, 3, [14, 3], [10, 4], [6, 7]] [51, 3, [25, 2], [17, 3], [8, 6]] [54, 3, [18, 3], [13, 4], [6, 9]] [55, 3, [27, 2], [11, 5], [5, 10]] [57, 3, [28, 2], [19, 3], [9, 6]] [60, 3, [20, 3], [12, 5], [7, 8]] [65, 3, [32, 2], [13, 5], [6, 10]] [66, 3, [22, 3], [16, 4], [6, 11]] [69, 3, [34, 2], [23, 3], [11, 6]] [70, 3, [17, 4], [14, 5], [10, 7]] [77, 3, [38, 2], [11, 7], [7, 11]] [78, 3, [26, 3], [19, 4], [6, 12]] [84, 3, [28, 3], [12, 7], [10, 8]] [85, 3, [42, 2], [17, 5], [8, 10]] [87, 3, [43, 2], [29, 3], [14, 6]] [91, 3, [45, 2], [13, 7], [7, 13]] [93, 3, [46, 2], [31, 3], [15, 6]] [95, 3, [47, 2], [19, 5], [9, 10]] [102, 3, [34, 3], [25, 4], [8, 12]] |
|
|
Quatre sommes jusqu'à 1000 [81, 4, [40, 2], [27, 3], [13, 6], [9, 9]] [162, 4, [54, 3], [40, 4], [18, 9], [13, 12]] [324, 4, [108, 3], [40, 8], [36, 9], [13, 24]] [625, 4, [312, 2], [125, 5], [62, 10], [25, 25]] [648, 4, [216, 3], [72, 9], [40, 16], [24, 27]] Cinq sommes jusqu'à 300 [45,
5, [22, 2], [15, 3], [9, 5], [7, 6], [5, 9]] [63, 5, [31, 2], [21, 3], [10, 6], [9, 7], [7, 9]] [75, 5, [37, 2], [25, 3], [15, 5], [12, 6], [7, 10]] [90, 5, [30, 3], [22, 4], [18, 5], [10, 9], [7, 12]] [99, 5, [49, 2], [33, 3], [16, 6], [11, 9], [9, 11]] [117, 5, [58, 2], [39, 3], [19, 6], [13, 9], [9, 13]] [126, 5, [42, 3], [31, 4], [18, 7], [14, 9], [10, 12]] [147, 5, [73, 2], [49, 3], [24, 6], [21, 7], [10, 14]] [150, 5, [50, 3], [37, 4], [30, 5], [12, 12], [10, 15]] [153, 5, [76, 2], [51, 3], [25, 6], [17, 9], [9, 17]] [171, 5, [85, 2], [57, 3], [28, 6], [19, 9], [9, 18]] [175, 5, [87, 2], [35, 5], [25, 7], [17, 10], [12, 14]] [180, 5, [60, 3], [36, 5], [22, 8], [20, 9], [12, 15]] [198, 5, [66, 3], [49, 4], [22, 9], [18, 11], [16, 12]] [207, 5, [103, 2], [69, 3], [34, 6], [23, 9], [11, 18]] [234, 5, [78, 3], [58, 4], [26, 9], [19, 12], [18, 13]] [243, 5, [121, 2], [81, 3], [40, 6], [27, 9], [13, 18]] [245, 5, [122, 2], [49, 5], [35, 7], [24, 10], [17, 14]] [252, 5, [84, 3], [36, 7], [31, 8], [28, 9], [12, 21]] [261, 5, [130, 2], [87, 3], [43, 6], [29, 9], [14, 18]] [275, 5, [137, 2], [55, 5], [27, 10], [25, 11], [12, 22]] [279, 5, [139, 2], [93, 3], [46, 6], [31, 9], [15, 18]] [294, 5, [98, 3], [73, 4], [42, 7], [24, 12], [14, 21]] [300, 5, [100, 3], [60, 5], [37, 8], [20, 15], [12, 24]] |
Six sommes jusqu'à 5000 [729,
6, [364, 2], [243, 3], [121, 6], [81, 9], [40, 18], [27, 27]] [1458, 6, [486, 3], [364, 4], [162, 9], [121,
12], [54, 27], [40, 36]] [2916, 6, [972, 3], [364, 8], [324, 9], [121,
24], [108, 27], [40, 72]] Sept sommes jusqu'à 300 [105, 7,
[52, 2], [35, 3], [21, 5], [17, 6], [15, 7], [10, 10], [7, 14]] [135, 7, [67, 2], [45, 3], [27, 5], [22, 6], [15,
9], [13, 10], [9, 15]] [165, 7, [82, 2], [55, 3], [33, 5], [27, 6], [16,
10], [15, 11], [11, 15]] [189, 7, [94, 2], [63, 3], [31, 6], [27, 7], [21,
9], [13, 14], [10, 18]] [195, 7, [97, 2], [65, 3], [39, 5], [32, 6], [19,
10], [15, 13], [13, 15]] [210, 7, [70, 3], [52, 4], [42, 5], [30, 7], [17,
12], [14, 15], [10, 20]] [231, 7, [115, 2], [77, 3], [38, 6], [33, 7],
[21, 11], [16, 14], [11, 21]] [255, 7, [127, 2], [85, 3], [51, 5], [42, 6],
[25, 10], [17, 15], [15, 17]] [270, 7, [90, 3], [67, 4], [54, 5], [30, 9], [22,
12], [18, 15], [13, 20]] [273, 7, [136, 2], [91, 3], [45, 6], [39, 7],
[21, 13], [19, 14], [13, 21]] [285, 7, [142, 2], [95, 3], [57, 5], [47, 6],
[28, 10], [19, 15], [15, 19]] [297, 7, [148, 2], [99, 3], [49, 6], [33, 9],
[27, 11], [16, 18], [13, 22]] [330, 7, [110, 3], [82, 4], [66, 5], [30, 11],
[27, 12], [22, 15], [16, 20]] |
|
Voir
Records
en quantité de sommes de consécutifs
|
Quantité
de partitions en nombres consécutifs |
|
|
Pour les
nombres de 1 à 1000. Les
nombres avec quantité 0 ou 1 ne sont pas indiqués. Par
exemple 45 a cinq partitions. [[9, 2], [15, 3], [18, 2], [21, 3], [25, 2], [27,
3], [30, 3], [33, 3], [35, 3], [36, 2], [39, 3], [42, 3], [45, 5], [49, 2], [50, 2], [51, 3], [54, 3], [55, 3],
[57, 3], [60, 3], [63, 5], [65, 3], [66, 3], [69, 3], [70, 3], [72, 2], [75,
5], [77, 3], [78, 3], [81, 4], [84, 3], [85, 3], [87, 3], [90, 5], [91, 3],
[93, 3], [95, 3], [98, 2], [99, 5], [100, 2], [102, 3], [105, 7], [108, 3],
[110, 3], [111, 3], [114, 3], [115, 3], [117, 5], [119, 3], [120, 3], [121,
2], [123, 3], [125, 3], [126, 5], [129, 3], [130, 3], [132, 3], [133, 3],
[135, 7], [138, 3], [140, 3], [141, 3], [143, 3], [144, 2], [145, 3], [147,
5], [150, 5], [153, 5], [154, 3], [155, 3], [156, 3], [159, 3], [161, 3],
[162, 4], [165, 7], [168, 3], [169, 2], [170, 3], [171, 5], [174, 3], [175,
5], [177, 3], [180, 5], [182, 3], [183, 3], [185, 3], [186, 3], [187, 3],
[189, 7], [190, 3], [195, 7], [196, 2], [198, 5], [200, 2], [201, 3], [203,
3], [204, 3], [205, 3], [207, 5], [209, 3], [210, 7], [213, 3], [215, 3],
[216, 3], [217, 3], [219, 3], [220, 3], [221, 3], [222, 3], [225, 8], [228,
3], [230, 3], [231, 7], [234, 5], [235, 3], [237, 3], [238, 3], [240, 3],
[242, 2], [243, 5], [245, 5], [246, 3], [247, 3], [249, 3], [250, 3], [252,
5], [253, 3], [255, 7], [258, 3], [259, 3], [260, 3], [261, 5], [264, 3],
[265, 3], [266, 3], [267, 3], [270, 7], [273, 7], [275, 5], [276, 3], [279,
5], [280, 3], [282, 3], [285, 7], [286, 3], [287, 3], [288, 2], [289, 2],
[290, 3], [291, 3], [294, 5], [295, 3], [297, 7], [299, 3], [300, 5], [301,
3], [303, 3], [305, 3], [306, 5], [308, 3], [309, 3], [310, 3], [312, 3],
[315, 11], [318, 3], [319, 3], [321, 3], [322, 3], [323, 3], [324, 4], [325,
5], [327, 3], [329, 3], [330, 7], [333, 5], [335, 3], [336, 3], [338, 2],
[339, 3], [340, 3], [341, 3], [342, 5], [343, 3], [345, 7], [348, 3], [350,
5], [351, 7], [354, 3], [355, 3], [357, 7], [360, 5], [361, 2], [363, 5],
[364, 3], [365, 3], [366, 3], [369, 5], [370, 3], [371, 3], [372, 3], [374,
3], [375, 7], [377, 3], [378, 7], [380, 3], [381, 3], [385, 7], [387, 5],
[390, 7], [391, 3], [392, 2], [393, 3], [395, 3], [396, 5], [399, 7], [400,
2], [402, 3], [403, 3], [405, 9], [406, 3], [407, 3], [408, 3], [410, 3],
[411, 3], [413, 3], [414, 5], [415, 3], [417, 3], [418, 3], [420, 7], [423,
5], [425, 5], [426, 3], [427, 3], [429, 7], [430, 3], [432, 3], [434, 3],
[435, 7], [437, 3], [438, 3], [440, 3], [441, 8], [442, 3], [444, 3], [445,
3], [447, 3], [450, 8], [451, 3], [453, 3], [455, 7], [456, 3], [459, 7],
[460, 3], [462, 7], [465, 7], [468, 5], [469, 3], [470, 3], [471, 3], [473,
3], [474, 3], [475, 5], [476, 3], [477, 5], [480, 3], [481, 3], [483, 7],
[484, 2], [485, 3], [486, 5], [489, 3], [490, 5], [492, 3], [493, 3], [494,
3], [495, 11], [497, 3], [498, 3], [500, 3], [501, 3], [504, 5], [505, 3],
[506, 3], [507, 5], [510, 7], [511, 3], [513, 7], [515, 3], [516, 3], [517,
3], [518, 3], [519, 3], [520, 3], [522, 5], [525, 11], [527, 3], [528, 3],
[529, 2], [530, 3], [531, 5], [532, 3], [533, 3], [534, 3], [535, 3], [537,
3], [539, 5], [540, 7], [543, 3], [545, 3], [546, 7], [549, 5], [550, 5],
[551, 3], [552, 3], [553, 3], [555, 7], [558, 5], [559, 3], [560, 3], [561,
7], [564, 3], [565, 3], [567, 9], [570, 7], [572, 3], [573, 3], [574, 3],
[575, 5], [576, 2], [578, 2], [579, 3], [580, 3], [581, 3], [582, 3], [583,
3], [585, 11], [588, 5], [589, 3], [590, 3], [591, 3], [594, 7], [595, 7],
[597, 3], [598, 3], [600, 5], [602, 3], [603, 5], [605, 5], [606, 3], [609,
7], [610, 3], [611, 3], [612, 5], [615, 7], [616, 3], [618, 3], [620, 3],
[621, 7], [623, 3], [624, 3], [625, 4], [627, 7], [629, 3], [630, 11], [633,
3], [635, 3], [636, 3], [637, 5], [638, 3], [639, 5], [642, 3], [644, 3],
[645, 7], [646, 3], [648, 4], [649, 3], [650, 5], [651, 7], [654, 3], [655,
3], [657, 5], [658, 3], [660, 7], [663, 7], [665, 7], [666, 5], [667, 3],
[669, 3], [670, 3], [671, 3], [672, 3], [675, 11], [676, 2], [678, 3], [679,
3], [680, 3], [681, 3], [682, 3], [684, 5], [685, 3], [686, 3], [687, 3],
[689, 3], [690, 7], [693, 11], [695, 3], [696, 3], [697, 3], [699, 3], [700,
5], [702, 7], [703, 3], [705, 7], [707, 3], [708, 3], [710, 3], [711, 5],
[713, 3], [714, 7], [715, 7], [717, 3], [720, 5], [721, 3], [722, 2], [723,
3], [725, 5], [726, 5], [728, 3], [729, 6], [730, 3], [731, 3], [732, 3],
[735, 11], [737, 3], [738, 5], [740, 3], [741, 7], [742, 3], [744, 3], [745,
3], [747, 5], [748, 3], [749, 3], [750, 7], [753, 3], [754, 3], [755, 3],
[756, 7], [759, 7], [760, 3], [762, 3], [763, 3], [765, 11], [767, 3], [770,
7], [771, 3], [774, 5], [775, 5], [777, 7], [779, 3], [780, 7], [781, 3],
[782, 3], [783, 7], [784, 2], [785, 3], [786, 3], [789, 3], [790, 3], [791,
3], [792, 5], [793, 3], [795, 7], [798, 7], [799, 3], [800, 2], [801, 5],
[803, 3], [804, 3], [805, 7], [806, 3], [807, 3], [810, 9], [812, 3], [813,
3], [814, 3], [815, 3], [816, 3], [817, 3], [819, 11], [820, 3], [822, 3],
[825, 11], [826, 3], [828, 5], [830, 3], [831, 3], [833, 5], [834, 3], [835,
3], [836, 3], [837, 7], [840, 7], [841, 2], [843, 3], [845, 5], [846, 5],
[847, 5], [849, 3], [850, 5], [851, 3], [852, 3], [854, 3], [855, 11], [858,
7], [860, 3], [861, 7], [864, 3], [865, 3], [867, 5], [868, 3], [869, 3],
[870, 7], [871, 3], [873, 5], [874, 3], [875, 7], [876, 3], [879, 3], [880,
3], [882, 8], [884, 3], [885, 7], [888, 3], [889, 3], [890, 3], [891, 9],
[893, 3], [894, 3], [895, 3], [897, 7], [899, 3], [900, 8], [901, 3], [902,
3], [903, 7], [905, 3], [906, 3], [909, 5], [910, 7], [912, 3], [913, 3],
[915, 7], [917, 3], [918, 7], [920, 3], [921, 3], [923, 3], [924, 7], [925,
5], [927, 5], [930, 7], [931, 5], [933, 3], [935, 7], [936, 5], [938, 3],
[939, 3], [940, 3], [942, 3], [943, 3], [945, 15], [946, 3], [948, 3], [949,
3], [950, 5], [951, 3], [952, 3], [954, 5], [955, 3], [957, 7], [959, 3],
[960, 3], [961, 2], [962, 3], [963, 5], [965, 3], [966, 7], [968, 2], [969,
7], [970, 3], [972, 5], [973, 3], [975, 11], [978, 3], [979, 3], [980, 5],
[981, 5], [984, 3], [985, 3], [986, 3], [987, 7], [988, 3], [989, 3], [990,
11], [993, 3], [994, 3], [995, 3], [996, 3], [999, 7], [1000, 3]] |
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Decompos/aaaDIVIS/NbPoli.htm
|
![]()