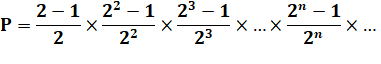|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
PUISSANCE de 2 Propriétés À retenir
|
|
2 n |
Nombres
polis ou
nombres escaliers |
|
2 p – 1 |
2 2 à l |
n 2 à l |
|
Fraction dyadique |
|||
|
|
2n+1 + (2n – 1) |
|
2n – 1 + n |
Voir Nombres binaires particuliers
/ Nombres 2-adiques / Types de nombres premiers
/
Puissances et exposants – Index
Amusements avec un nombre en puissances de 2
|
1 / 998 = 0,001 002 004 008 016 032 064 128 256
513 026 052 104 208 416 833 667
….3 Suite des puissances de 2 jusqu'à 256 = 28. |
|
Application d'une identité remarquable avec les
puissances de 2:
|
Voir Motifs sur les racines carrés
|
Rectifier
l'opération en déplaçant un seul chiffre.
|
Relations
entre puissances de 2

Tous
ces nombres sont des repunits
en binaire.
Ex: 63 = 1111112
Voir Identités remarquables en An – 1
|
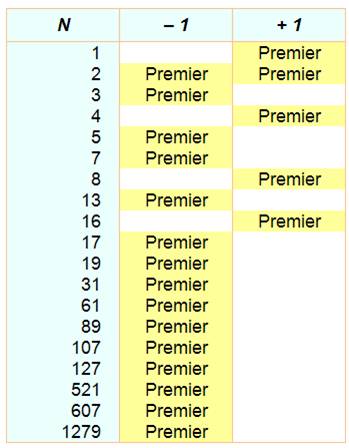
Liste
des nombres n tels que n – 2k positif sont tous premiers. [1, 7, 15, 21, 45, 75, 105] Exemple: 105 => 103, 101,
97, 89, 73, 41 sont premiers |
|
4 = 30 +
31 et 256 = 30 + 31 + 32
+ 35 Seuls cas connus d'une puissance de 2 égale
à une somme de puissances de 3 distinctes. Aucune en puissance de 5. Avec la
puissance 7, on a le seul cas de 8 = 70
+ 71. |
![]()
|
|
||
|
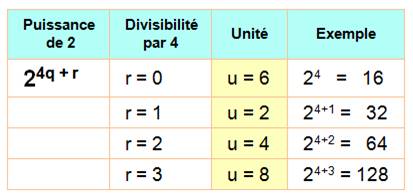
Rappel des puissances
de 2: |
2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048 … |
|
|
Les unités se répètent
selon un cycle de longueur 4: |
2, 4, 8, 6 |
|
|
Les deux derniers chiffres se répètent selon un cycle
de longueur 20: |
4, 8, 16, 32, 64,
28, 56, 12, 24, 48, 96, 92, 84, 68, 36, 72, 44, 88, 76, 52 |
|
|
Les trois derniers chiffres se répètent selon un
cycle de longueur 100: |
8, 16, 32, 64,
128, 256, 512, 24, 48, 96, 192, 384 … |
|
|
Lp est la longueur de la période pour m derniers
chiffres. La période commence à partir de 2m. |
Lp = 4 . 5m – 1 |
|
|
Bilan pour m
successifs de 1 à 10: |
4, 20, 100, 500,
2 500, 12 500, 62 500, 312 500, 1 562 500, 7 812 500 |
|
|
Les puissances
négatives de 2 se terminent alternativement par 125 et 625, sauf les deux
premières. |
|
|
Voir Table
des puissances de 2 avec mise en évidence des derniers chiffres /
Programmation de la
recherche des derniers chiffres d'une puissance de n /
|
ne
sont pas sommes de consécutifs |
|
|
|
La partition des puissances de 2 avec des
nombres consécutifs est impossible. |
Exemple 24 = 16 Parmi les 231 partitions du nombre 16, aucune n'est
somme de deux nombres consécutifs ou plus. |
|
Voir Les puissances de 2 sont des nombres
2-friables
|
sont
presque parfaites |
|
|
|
Toutes les puissances de 2 sont presque parfaites (déficience
égale à 1). Anglais: least deficient or near-perfect numbers. |
Exemple 24 = 16 Diviseurs
propres: 1, 2, 4, 8 Somme:
15 Soit
une déficience de 1. |
|
|
|
||
|
Numération Comme les puissances de 10 sont à la base du
système décimal, les puissances de 2 sont à la base du système de numération binaire Remarque 1112 = 710 = 22
+ 21 + 20 10002 = 810 = 23 Plus généralement 2n
– 1 = 11 …11 en binaire 2n = 1 00 …00 en binaire |
10112 = 1 x 23
+ 0 x 22 + 1 x 21 + 1 x 20 = 8 + 0 + 2 + 1 = 1110 Toutes les puissances de 2 de 0
à 4. n fois le 1 Un 1 et n fois le 0 |
|
|
Les
unités des puissances de 2 se répètent
selon un cycle de quatre valeur: 2, 4, 8, 6. Soit le tableau résumé suivant:
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Observations
Exemple développé avec
S9
Théorèmes La somme des
puissances de 2 est égale à la puissance de deux
suivante moins 1. Sn = 2n+1
– 1 Une puissance de deux
est égale à la somme de toutes les puissances
de deux inférieures plus un. 2n+1
= Sn + 1 2n = Sn-1
+ 1 Exemple
Formulation
Voir Somme des puissances / Identité remarquable
EN Résumé: suites
géométriques de raison 2 et 1/2
Ce
sont effectivement deux suites
géométriques dont on connait immédiatement la somme. Pour l'exemple, on
va tout de même en étudier quelques démonstrations. |
|||||||||||||||||||||||||||||||||||||||||||||||||
Voir Variations
sur les sommes / Nombre presque-parfaits / Compter les parties de tennis
Puissances de 2 et divisibilité par 3
|
La somme de deux puissances de 2 consécutives est
divisible par 3. C'est vrai également pour la concaténation
|
Suite Puissances de 2 et divisibilité par 3
/ Brève
de math 491
|
Démonstration par induction |
|
|
|
|
Sn = 2n-1
+ 2n-2 + … + 2 + 1 = 2n
– 1 |
|
|
|
Sn+1 = 2n +
2n-1 + 2n-2
+ … + 2 + 1 Sn+1 = 2n +
Sn |
|
|
|
Sn+1 = 2n +
2n – 1 |
|
|
|
Sn+1 = 2n+1 – 1 |
|
|
|
Si
la formule est vraie pour n, elle est vraie pour n+1 |
|
|
|
S0
= 20 = 1 = 21
– 1 = 2 – 1 = 1 |
|
|
Or
vraie pour 1 Donc
vraie dans tous les cas. |
||
Voir Démonstration
par induction
|
Démonstration par sommes |
|
||
|
|
2n = 2n (2
– 1) 2n = 2n+1 – 2n |
||
|
|
Sn = 2n
+ 2n-1 + 2n-2 +
… + 2 + 1 |
||
|
On
se souviendra que 20 = 1. (Voir Explication) |
Sn = 2n + 2n-1 + 2n-2 + … + 21 + 20 |
Sn = 2n+1
– 2n +
2n – 2n-1 +
2n-1 – 2n-2 + … +
22 – 21 +
21 – 20 |
|
|
|
Sn = 2n+1
– 20 =
2n+1 – 1 |
||
|
|
||
|
2n
=
2 x 2 x … 2 |
|
|
|
22n = 3k + 1 |
|
|
|
22n+1
=
3k + 2 |
|
|
|
Illustration
|
||
Voir Divisibilité des puissances de
2 / Divisibilité des puissances de 2 moins
unité
|
|
|
|
La somme des
coefficients de la ligne n
du triangle de Pascal vaut 2 n.
Explications
2 = 1 + 1
|
|
|
|
||||
|
Montrez que |
2n |
> 2n pour n > 2 |
||
|
Point de départ |
23 |
= 8 > 2 x 3 = 6 Vrai pour 3 |
||
|
Hypothèse |
2k |
> 2k |
||
|
Démontrez sous cette hypothèse |
2k + 1 |
> 2 (k + 1) |
||
|
Développement de la puissance |
= 2 x 2k |
|||
|
Selon l'hypothèse |
> 2 x 2k |
|||
|
Factorisation |
> 2 (k + 1) |
|||
|
Induction |
Propriétée vraie pour k = 3. Propriétée rai pour k + 1
si vraie pour k Alors, toujours vraie pour n > 2. |
|||
Voir Démonstration
par induction
|
|
||||
|
Montrez que |
2n |
> n3
pour n > 9 |
||
|
Point de départ |
210 |
= 1024 > 1000 Vrai pour 10 |
||
|
Hypothèse |
2k |
> k3 |
||
|
Démontrez sous cette hypothèse |
2k + 1 |
> k3 + 1 |
||
|
Développement de la puissance |
= 2 x 2k |
|||
|
Selon l'hypothèse |
> 2 x k3 |
|||
|
Explicitation |
> k3
+ k3 > k3
+ k . k2 |
|||
|
Minoration pour nous arranger |
> k3
+ 7 . k2 > k3
+ 3 . k2 + 3 . k2 + k2 > k3
+ 3 . k2 + 3 . k + 1 |
|||
|
> (k + 1)3 |
||||
|
Induction |
Propriétée vraie pour k = 10 Propriétée rai pour k + 1
si vraie pour k Alors, toujours vraie pour n > 9. |
|||
|
|
|||
|
Plus grand nombre avec
3 deux |
42 = 24 = |
16 |
|
|
222 = |
222 |
||
|
22² = |
484 |
||
|
2²² = |
4 194 304 |
||
|
Plus grand nombre avec
4 deux |
2 222 |
10
3 |
|
|
222 ² = 49 284 |
10
4 |
||
|
= 65 536 |
10
5 |
||
|
|
10
14 |
||
|
22 ²² |
10
29 |
||
|
2 ²²² |
0,67
10 67 |
||
|
|
0,5
10 146 |
||
|
|
10
1 262 612 |
||
Voir Échecs
/ Tour de Brama ou de Hanoi
|
|
|
|
267 – 1 = 1, 47… 10 20 = 147 573 952 589 676 412 927 = 193 707 721 x
7 618 388 257 287
Voir Ce nombre Anecdote: Frank Cole est
professeur de mathématiques à l'université Columbia de New York. En 1903,
lors d'une cession de la Société mathématique américaine, sans dire un mot,
il écrit au tableau le nombre de Mersenne 267 – 1, puis sur
l'autre tableau le produit de deux nombres, et, enfin, entre les deux le
signe égal. Il avait passé trois années de ses temps libres pour arriver à
factoriser ce nombre. |
|
À noter
|
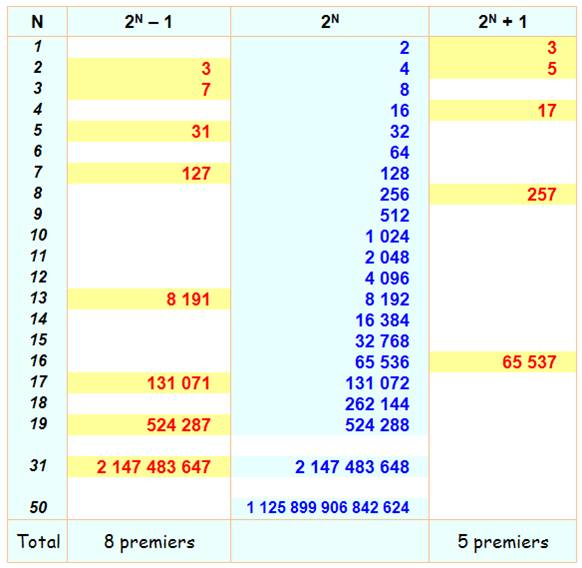
Pour tout n
entier > 1 on n'a jamais n Une infinité de
nombres sont tels que n Une infinité de nombres sont tels que n
|
|
PUISSANCE DE 2 |
|
|
Pour
N <50
Pour
N >50
Vérifié jusqu'à
1900 Suite en Nombres
de Mersenne
|
|
Voir Machine à factoriser des
frères Carissan
Divisibilité par n de 2n + 1,
etc.
|
Les exposants n suivants sont tels que n divise 2n
+ 1: 1, 3, 9, 27, 81, 171, 243,
513, 729, 1539, 2187, 3249, 4617, 6561, 9747, 13203, 13851, 19683, 29241,
39609, 41553, 59049, 61731, 87723, 97641, 118827, 124659, 177147, 185193,
250857, 263169, 292923, 354537, 356481, 373977, 531441, 555579, 752571,
789507, 878769, … Les exposants n suivants sont telles que n divise
2n + 2: 1, 2, 6, 66, 946, 8646, … Les exposants n suivants sont telles que n divise
2n + 3: 1, 5, 917, 3223 Avec 2n – 1 : ces nombres ne sont
jamais divisibles par n (sauf n = 1). |
|
|
|
|
Équation
Exemples
Équation
amusante découverte et démontrée
en 1986 par Pascal Peyremorte |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
1
125 899 906 842 624 = 1,126 10 15 morceaux de papier plié. On
prend une feuille de papier à cigarette de 1/50 mm (très fin!). il
en faut 500 pour faire 1 cm d'épaisseur. On
déchire la feuille en deux et on empile les morceaux. On
recommence l'opération 50 fois. Quelle est la
hauteur de la pile?
Distance
à comparer à (en km)
|
|||||||||||||||||||||||||||||||||||||||||||
Voir Périmètre
du papier plié / Timbres / Feuille pliée - Débutant / Courbe du dragon
|
|
|
|
Produit infini avec les puissances de 2.
Euler a montré
que de produit peut être calculé plus facilement avec la somme infinie: 1 – x – x2 + x5 + x7 – x12
– x15 + x22 + x26 – x35 – x40
+ … Les exposants sont les nombres pentagonaux généralisés:
n(3n – 1 ) / 2 avec n = 0, +1, -1, +2, -2 … |
|
Voir Sommes
de suites qui rendent fou
|
2, 3, 9, 13, 19, 21, 55, 261, 3 415, 4 185, 7
353, 12 213 … |
|
Rectifier
l'opération en déplaçant un seul chiffre.
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |