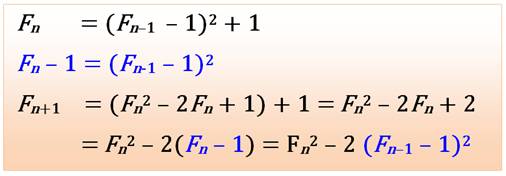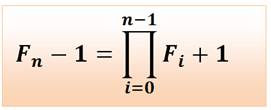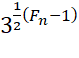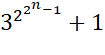NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 24/02/2012 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	PUISSANCE de 2
Débutants Puissance	Nombres de Fermat et Mersenne			Glossaire Puissance
INDEX Puissance Décomposition Puissance de 2		FERMAT (biographie)	MERSENNE (biographie)
		Nombres de Fermat	Nombres de Mersenne
		Valeurs et facteurs	Valeurs et facteurs
		Diviseurs
		Sommaire de cette page >>> Nombres de Fermat >>> Propriétés >>> Construction >>> Curiosités >>> Fermat généralisés >>> Fermat se terminent par 7 >>> Fermat et 2

NOMBRES de FERMAT

Fermat croyait qu'en ajoutant 1 à ces puissances de 2,

on obtenait toujours des nombres premiers.

Or, selon les connaissances d'aujourd'hui, seuls cinq sont premiers.

NOMBRES de FERMAT
Forme générale Fn = Dn + 1 Autres notations: Fn = 2^2^n = 2^(2^n) Calcul F3 – 1 = 2^2^3 = 2^8 = 256 F3 = 257 Formation

Voir Puissances à étages / Divisibilité par 3 de tels nombres en +2 (et non +1)

Valeurs

Suite >>>

Relations entre deux voisins

Voir Formation des nombres de Fermat

Relations entre tous les précédents Autre expression Fn = F0 F1 F2 .... Fn-1 + 2 Exemples F3 = F0 F1 F2 + 2 = 3 x 5 x 17 + 2 = 257 F4 = 3 x 5 x 17 x 257 + 2 = 65 537 Démonstration par induction (>>>)
Pour F1 c'est vrai.	5 – 3 = 2 F1 – F0 = 2
Supposons la formule vraie pour n	Fn – 2 = F0 . F1 . F2 … Fn-1
L'est-elle pour n + 1?	Fn+1 – 2 = F0 . F1 . F2 … Fn-1 . Fn = (Fn – 2) . Fn
En remplaçant par leur valeur. Identité remarquable >>> Carré d'une puissance en 2 >>> Passage de – 1 à + 1 – 2 Reconnaissance du nombre de Fermat

Curiosité à 2 près (Normale, si on connaît la propriété ci-dessus!)

4 294 967 295 = 3 x 5 x 17 x 257 x 65 537 Le produit des 5 nombres premiers de Fermat connus.

4 294 967 297 = 641 x 6 700 417 Le nombre de Fermat suivant qui n'est pas un nombre premier

Propriétés des NOMBRES de FERMAT

Les cinq plus petits nombres de Fermat (n de 0 à 4) sont premiers. Suite >>> À partir de F2, tous les nombres de Fermat se terminent par 7. Suite >>> Deux nombres de Fermat sont premiers entre eux. Tout diviseur de Fn est de la forme 2^m k + 1 avec k impair et m n + 2. Suite >>> Aucun nombre de Fermat n'est triangulaire (sauf 3), ni carré, ni cube. Un nombre de Fermat est premier si, et seulement si, il divise: ou (test de Pépin – 1877) Il n'est possible de construire un polygone régulier à nombre premier de côtés que si ce nombre est un nombre de Fermat premier. Gauss Aucun nombre de Fermat n'est somme de deux nombres premiers à l'exception de F1 = 2 + 3. Aucun nombre de Fermat n'est la différence de deux puissances de nombres premiers impairs. La somme des inverses de tous les nombres de Fermat est irrationnelle.

NOMBRES en puissance de 2
Puissance	Nombres de Mersenne	Nombres de Sierpinski	Nombres de Fermat	Nombres de Fermat généralisé
>>>	>>>	>>>	>>>	>>>

NOMBRES de FERMAT – Unité 7
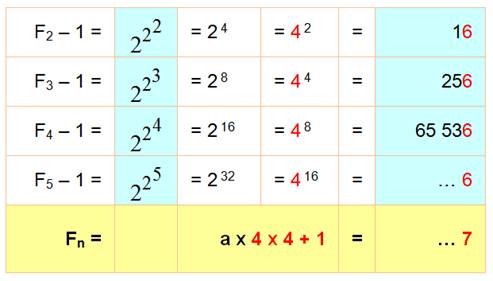
À partir de F2, tous les nombres de Fermat se terminent par 7. Exemple et quasi-démonstration Démonstration par induction (>>>)
Pour n =1, c'est faux, mais Pour n = 2, c'est vrai. Supposons la formule vraie pour n. L'est-elle pour n + 1? Calcul avec relation puissance de 2. Mise en évidence du Fermat précédent.
Passage aux congruences (modulo), en prenant pour vraie la formule pour Fn.	Fn+1 (( 7 ) – 1)² + 1 mod 10 ≡ 6² + 1 = 37 mod 10 ≡ 7 mod 10
La relation est vraie pour 2 et elle est vraie pour n+1 dès qu'elle est vraie pour n, alors elle est toujours vraie pour n à partir de 2

Suite	Valeur de Fn Diviseurs de Fn
Voir	Mersenne Harshad Théorie des nombres – Index Nombres par leur nom
DicoNombre	Nombre 3 Nombre 5 Nombre 17 Nombre 257
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Decompos/Fermat.htm