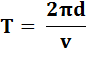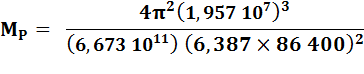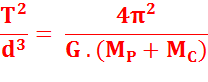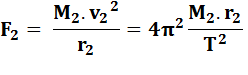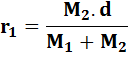NOMBRES - Curiosités, théorie et usages

 

Accueil                           DicoNombre            Rubriques           Nouveautés      Édition du: 05/08/2014

Orientation générale        DicoMot Math          Atlas                   Références                     M'écrire

Barre de recherche          DicoCulture              Index alphabétique                               

     

Astronomie

 

Débutants

Général

Calculs

 

Glossaire

Général

 

 

INDEX

 

Astronomie

 

Sciences 

Pluton et Charon

Première

 

Sommaire de cette page

>>> Les données

>>> Interaction gravitationnelle

>>> Mouvement de Charon

>>> Masse de Pluton

>>> Masse à prendre en compte

>>> Newton et Kepler

>>> Troisième loi de Kepler

 

 

 

 

 

PLUTON & CHARON

Calcul de masse

 

Exercice de calcul pour se familiariser avec les lois de Newton. Un exercice de ce type fut donné au baccalauréat en 2008.

En fait, Pluton et Charon  sont plutôt des planètes doubles; elles tournent ensemble autour d'un point commun. Charon paraît donc immobile dans le ciel plutonien. 1978, découverte de Charon.

Charon, dans la mythologie, est le passeur des Enfers dont Hadès est le dieu, appelé Pluton chez les Romains.

 

 

 

Les données

Général

 

 

*    Constante de gravitation universelle

6,673 1011

m3. kg-1. s-2

*    Année sidérale

365,256 4

jours

*    Jour solaire moyen

86 400

secondes

Pluton

 

 

*    Rayon

1,153 103

km

*    Distance moyenne au Soleil

5,906 45 109

km

*    Période de révolution autour du Soleil

90 613,3058

248a   31j   7,34h

jours

 

Charon

 

 

*    Rayon

6,036 102

km

*    Distance moyenne au centre de Pluton

1,957 104

km

*    Période de rotation (sur lui-même)

6,387

jours

*    Période de révolution autour de Pluton

6,387

jours

*    Masse

1,52 1021

kg

 

 

Hypothèses principales

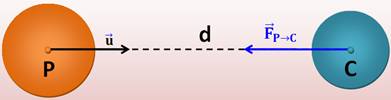
Mouvement circulaire uniforme: la trajectoire suivie est un cercle (rayon R) et la valeur de la vitesse (v) est constante au cours du mouvement. Alors:

*    le vecteur accélération est radial et centripète:

*    la valeur de a est constante.

Référentiel galiléen: attaché à Pluton avec pour origine le centre de Pluton (P). On ne considère que les interactions entre Pluton et Charon, en négligent toutes les autres possibles comme celle du Soleil par exemple.

 

 

 

Interaction gravitationnelle

 

*    Deux corps (planètes) P et C sphériques, homogènes en masse.

*    Centre de gravité en P et C, centre des sphères.

*    Distance d entre les deux centres.

*    Masses Mp et Mc.

 

 

 

*    Force d'attraction ou d'interaction gravitationnelle exercée par le corps P sur le corps C

 

 

Mouvement de Charon

*    Charon : mouvement circulaire uniforme, d'accélération a autour de Pluton.

 

*    Deuxième loi de Newton, appliquée au centre d'inertie C de Charon dans le référentiel de Pluton, supposé galiléen.
(masse de Charon négligée)

 

*    En reprenant l'expression de la force:

*    D'où la valeur de l'accélération:
(qui ne dépend pas de la masse de Charon)

*    Accélération:                          Direction

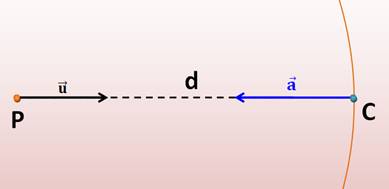
Sens

Norme

La droite Pluton – Charon

de Charon vers Pluton

a = G. Mp / d²

*    Expression de l'accélération d'un mouvement circulaire uniforme:

*    En rapprochant les deux expressions de a:

*    Soit l'expression de la vitesse de Charon.

*    Charon fait le tour de Pluton en un temps T. Avec la relation L = v.t, on trouve:

 

 

 

*    Nous connaissons la vitesse:

 

*    Sous cette forme, cette relation est la troisième loi de Kepler ou loi des périodes

 

 

 

Masse de Pluton

*    Elle se déduit de la formule précédente:

*    Application numérique:

*    Valeurs:

 

Num = 2,998 … 1022

Déno = 20,3208 …

Mp = 1,47533 … = 1,456 … 1022 kg

 

*    En fait, il aurait fallu faire intervenir la masse de Charon avec cette formule:

*    Valeur corrigée

 

 

 

Masse de Pluton

 

Deux valeurs de la masse: 1, 456 ou 1, 304 en 1022 kg

pour une valeur connue en 2014  de:

 

1, 314   0,018  en 1022 kg  soit entre 1,296 et 1,332.

Moins de 0,24% celle de la Terre

 

 

 

Masse à prendre en compte

 

*    La formule est souvent utilisée avec le Soleil et une planète. Il est alors très justifié de négliger la masse de la planète face à celle du Soleil.

*    Jupiter représente 1/1000 de la masse du Soleil. Négligeable.
Quant à Charron, c'est seulement 1/10 de la masse de Pluton. Non négligeable.

 

 

 

 

Newton et Kepler

 

*    Deux corps M1 et M2

Leur centre de gravité: G à des distances r1 et r2 de ces deux corps.

*    L'attraction gravitationnelle s'exerce sur la ligne M1M2. De sorte que ces deux corps exécutent une rotation dans la même période de temps (T); mais pas à la même vitesse.

 

*    Évaluation de ces forces.

On reprend une partie des calculs effectués ci-dessus.

 

 

 

*    Selon la troisième loi de Newton: égalité: F1 = F2, ce qui induit, simplification faite:

 

 

Le corps le plus massif orbite plus près du centre de gravité.

 

*    Soit la valeur de la distance de l'un des corps au centre de gravité:

 

 

 

*    En reprenant l'expression de la force et en donnant la valeur de la période:

 

 

*    Loi de Newton sur la gravitation:

*    En remplaçant:

 

 

 

 

 

Troisième loi de Kepler ou loi des périodes

 

Bilan

Si une planète gravite autour d'une étoile, la rotation se fait autour du centre de masse commun au deux corps, et les deux objets bougent comme le lanceur de marteau et son marteau. Plus la planète est grande et proche de son étoile et plus le mouvement de l'étoile sera grand.  L'observation de petit mouvement de l'étoile est suffisante pour suspecter la présence d'une exoplanète.

Voir Historique Uranus et Mercure

 

 

 

 

 

 

 

Suite

*    Amas / Groupe local

*    Pluton

*    Lois de Newton

Voir

*    Andromède

*    Cosmologie – Glossaire et index

*    Dimensions dans l'univers

*    Distances en km et en secondes-lumière

*    Étoiles

*    La Galaxie

*    Sciences – Index

*    Soleil

Cette page

http://villemin.gerard.free.fr/Cosmogra/aCalcul/Charon.htm