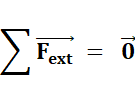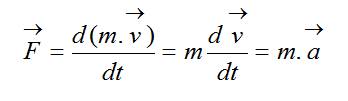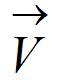NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 01/05/2019 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Physique
Débutants Général	Dynamique				Glossaire Général
INDEX Sciences	Lois de Kepler	Principe de Galilée		Lois de Newton
	Sommaire de cette page >>> Approche >>> Révolution de pensée >>> Historique >>> 1 - Loi de l'inertie >>> 2 - Loi fondamentale >>> 3 - Loi des actions réciproques >>> Bilan >>> Quantité de mouvement >>> Quatre concepts

La célèbre POMME de Newton

Sans doute une légende !?

Bien avant la naissance de Newton, le principal problème de la navigation était de déterminer sa longitude. Pour une nation commerçante, l'Angleterre se devait de trouver un moyen de mesurer la longitude en mer qui passait par la mesure précise de l'angle entre la Lune et des étoiles fixes (méthode d'Amerigo Vespucci – 1498; celui qui a laissé son nom à l'Amérique). Or la Lune présente des anomalies de comportement pas faciles à formaliser. Le Bureau de la longitude anglais offre un prix à qui précisera le mouvement de la Lune. Newton s'y atèle et décrit le mouvement des planètes, de la Lune; traite de l'accélération de la pesanteur, des marées et de la variation des chronomètres durant les voyages en mer (troisième livre des Principia).

D'après: Histoire populaire des sciences – Clifford Conner – Page 465

Voir Pensées & humour

LOIS DE NEWTON

Elles sont trois, et assez connues de tous.

Mais à l'époque, c'était une révolution conceptuelle.

Aujourd'hui, elles font toujours phosphorer les savants dès que l'on atteint trois corps ensemble.

Équations simples à énoncer, complexes dans leurs solutions.

Anglais: The three laws of motions

APPROCHE – Les trois lois, simplement
1	2	3
Si j'avance, j'avance sans fin.	On me pousse, j'accélère.	Celui qui me pousse, recule.
Dans la réalité les frottements et la résistance de l'air me font ralentir.	Une poussée me fait prendre de la vitesse, ou me fait changer de direction, ou me fait avancer si j'étais au repos.	Une poussée vaut à mon pousseur une même poussée dans l'autre sens.
Cas du patineur sur la glace. D'une boule sur un billard. Les planètes tournent autour du Soleil sans se fatiguer. Une roue montée sur un excellent roulement à billes semble tourner inlassablement.	La voiture accélère grâce à la poussée de son moteur. Une pierre lâchée dans un puits se met à tomber de plus en plus vite sous l'effet de la pesanteur.	Cas flagrant du recul du fusil. ou de la barque qui s'éloigne du bord lorsque, étant dessus, on saute sur la berge.

RÉVOLUTION DE PENSÉE Caractéristiques d'un objet en mouvement
Traditionnel	Avec Newton
Position Vitesse Masse	Position Quantité de mouvement = masse x vitesse p = m . v Deux variables suffisent pour décrire un système dynamique.
Voilà l'astuce, cela paraît simple, mais il fallait y penser. NB: les relations sont vectorielles.

Nouvelle vision des trois lois
1	2	3
Seul dans la nature, je conserve ma quantité de mouvement.	Une force motrice modifie ma quantité de mouvement, mon comportement.	On conserve la quantité de mouvement globale: moi + apport externe.
P = M .V = constante	F modifie p	P = M .V = constante
C'est constant.	Seule une force peut modifier.	Mais le global reste constant. Cette 3^e loi est la même que la 1^ère, mais généralisée.

HISTORIQUE

Galilée, Descartes, Gassendi … connaissaient plus ou moins ces lois. C'est à Newton que revient l'honneur de les avoir rassemblées et formulées. Elles sont la base de la mécanique. La découverte du concept de la quantité de mouvement donne une véritable "impulsion" à cette science. Newton disait: La quantité de mouvement est la mesure que l'on tire à la fois de sa vitesse et de sa quantité de matière. En 1687, Newton publie ses trois lois dans son ouvrage: "Principia" Philosophiae naturalis principia mathematica Principes mathématiques de philosophie naturelle Modèle de didactisme (comme l'avait été Euclide dans les Éléments). Encensé par Halley. Énorme impact !

Première loi: LOI DE L'INERTIE
Loi	Tout corps persévère dans l'état de repos ou de mouvement uniforme en ligne droite, sauf si quelque chose le contraint à changer d'état.
Bof !	Contraire à l'observation quotidienne: En vélo, même lancé, il faut continuer à pédaler pour avancer. Une pierre qui roule finit par s'arrêter.
Mais si …	Cette loi au contraire dit que: Aucune force n'est nécessaire pour entretenir un mouvement. Sans contraintes, le mouvement continue sans fin, à la même vitesse et en ligne droite. Les contraintes: résistance de l'air, frottements …
Formulation	Dans tout référentiel galiléen, le centre d'inertie d'un système pseudo-isolé a un vecteur-vitesse constant. Soit: est équivalent à

La Terre dans le référentiel Terre est un système pseudo-isolé: son centre d'inertie y est immobile.

La Terre dans le référentiel Soleil n'est pas un système pseudo-isolé: le centre d'inertie de la Terre parcourt une ellipse.

Deuxième loi: Relation fondamentale de la dynamique
Loi	Les changements de mouvement sont proportionnels à la force motrice et se font dans le sens de la force appliquée.
Ouille !	C'est la loi la plus difficile à comprendre. Mais aussi la plus fondamentale. Celle qui dit comment les choses peuvent évoluer: il faut une force motrice.
Général	L'action d'une force fait varier: proportionnellement la quantité de mouvement (m . v). Son application générale avec modification à la fois de la masse et de la vitesse se trouve, par exemple, dans le cas des fusées qui décollent.
Particulier	Dans une majorité de cas classiques: La masse est constante. Seule la vitesse varie, et L'accélération est proportionnelle à la force.
Formulation	Dans un référentiel galiléen, la somme vectorielle F des forces appliquées à un point matériel est égale à la dérivée par rapport au temps du produit de sa masse par son vecteur vitesse. Soit Accélération (a) = variation de la vitesse, c'est-à-dire dérivée de la vitesse par rapport au temps.
Chute	Un solide en chute libre n'étant donc soumis qu'à son poids; l'accélération de son centre d'inertie est égale au vecteur champ de pesanteur:

Voir Application au calcul de l'orbite géostationnaire / Mouvement de Charon

Troisième loi: Loi des actions réciproques, ou Loi de l'action et de la réaction ou Loide la conservation de la quantité de mouvement
Loi	À toute action est opposée une réaction égale; Ou Les actions de deux corps sont réciproques.
Générale	En l'absence de forces extérieures, la quantité de mouvement d'un système reste constante.
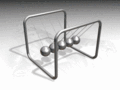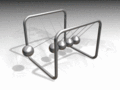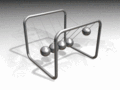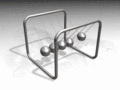
Ouille !	Souvenez-vous des gadgets* de salon avec des billes côtes à côte: On écarte l'une d'elles; C'est la dernière en ligne qui part; Celles du milieu restent immobiles; Et celle qui est venue les frapper s'arrête net! La quantité de mouvement de la première à été transmise intégralement à la dernière. La quantité de mouvement est restée constante. * Pendule de Newton (Newton's cradle or pendulum)
En fait	On se retrouve la première loi non pas sur un corps seul mais sur un système global.
Formulation	Lorsqu'un système S exerce une force FSS' sur un système S', alors S'exerce sur S une force FS'S ayant même droite d'action. Avec

BILAN

Résumé illustré La pierre qui tombe La pierre qui tombe est soumise à la force de gravitation: elle accélère sans arrêt; elle tombe de plus en plus vite bien que freinée par la résistance de l'air; jusqu'à atteindre une vitesse limite lorsque cette résistance devient grande. La planète qui tombe La planète qui tombe est soumise à la force de gravitation: elle est attirée par le Soleil sans autre effet, elle s'écraserait sur l'astre brûlant; mais, elle avait une trajectoire initiale qui l'éloigne dans l'espace; le Soleil agit en "appelant" la planète vers elle ce qui a pour effet de courber la trajectoire initiale. Imaginez que l'effet ne se produise que de temps en temps: la planète avance en ligne droite le soleil la fait chuter un peu; elle continue sa trajectoire en ligne droite le soleil inlassablement la rappelle un peu; on voit se dessiner une trajectoire en polygone. En fait, le phénomène est continu, et la trajectoire est une ellipse.

Quantité de mouvement Impulsion Résultante cinétique
un point M de masse m et de vecteur vitesse	La quantité de mouvement ou impulsion est le vecteur:
La quantité de mouvement ou résultante cinétique d'un système formé de points est la somme des quantités de mouvement de chaque point. Elle est égale à la quantité de mouvement d'un point matériel placé au centre d'inertie de masse égale à la somme des masses de chaque point. La dérivée de la quantité de mouvement d'un système est égale à la somme des forces qui lui sont appliquées Si la masse est constante, alors la dérivée de la quantité de mouvement (m.v) est simplement la dérivée de la vitesse, soit l'accélération (a), et F = m . a

Anglais: Momentum

Résumé

1	Forces	Position	Vitesse	Accélération
	ÉQUILIBRÉES	a) – Repos	0	0
		b) – Mouvement Uniforme	V = Constante	0

2	Forces	Position	Vitesse	Accélération
	NON ÉQUILIBRÉES	Mouvement accéléré	V croît ou décroît	a = f (F)
				a = 1 / f(m)

Quatre concepts de Newton

Quatre concepts synthétisent les lois de la physique classique de Newton: Concept d'espace et de temps absolus, et d'objets séparés se déplaçant dans l'espace et interagissant les uns sur les autres; Concept de forces fondamentales, différentes de la matière; Concept de lois fondamentales décrivant le mouvement et les interactions des objets; et Concept de déterminisme et de description objective de la nature basée sur la division cartésienne de l'esprit et de la matière.

Suite	Attraction de la Terre Gravitation – Index Quatre concepts de Newton Calcul de la masse de Pluton Newton Traversée de la Terre – Calculs
Voir	Balle contre un mur Culture générale Jeux – Index La pomme attire la Terre Lois de Kepler Masses Mécanique – Glossaire Mécanique quantique Mécanique relativiste Paradoxe de Galilée Pendule de Foucault Physique amusante Projectile Relativité Sciences – Index
DicoNombre	Nombre 4
Sites	Les lois de Newton par Y Weiss Isaac Newton et ses lois par Sébastien Charnoz Newtonium Voir les orbites interactives (un peu long à charger) Lois de Newton et astronomie Lois de l'attraction universelle par Benoît Tournerie
Cette page	http://villemin.gerard.free.fr/Scienmod/NewtLois.htm