|
|||||||||||||||||||||||||||||
![]()
|
Diagramme (ou tableau) de KARNAUGH ou Diagramme
de VEITCH-KARNAUGH Moyen graphique commode de
pour représenter des fonctions logiques. Analyse de toutes les possibilités logiques
de plusieurs variables et optimisation des fonctions. |
Anglais: Karnaugh
map
Voir Biographies
de Maurice Karnaugh et de Edward Veitch
|
|
|
|
Principe
Définition
Diagramme de KARNAUGH
Lecture
|
|
|
|
|
|
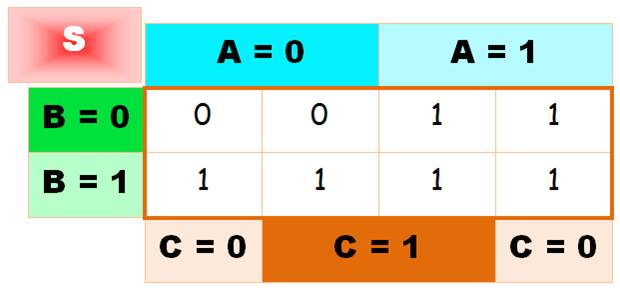
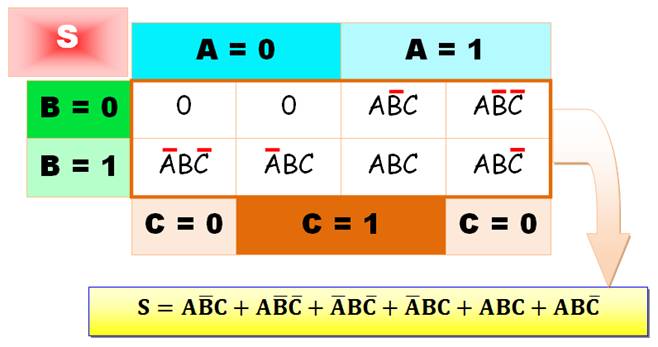
Énoncer tous les cas
Regroupement (optimisation)
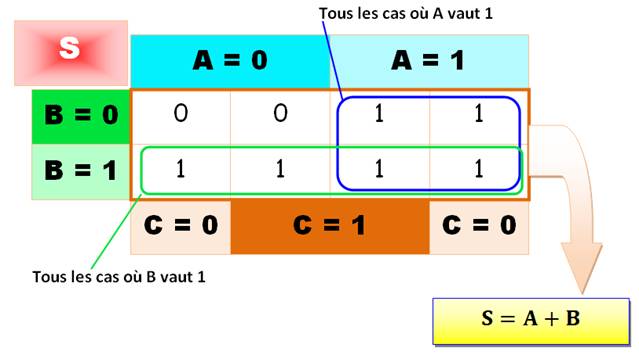
Voyez comme sur cet exemple simple la fonction de
sortie se résume à S = A ou B. Dès que
A ou B est à 1 (ou les deux à la fois), la fonction de sortie est à 1
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
F = A.B.nC.nD + A.B.nc.D |
Conventions: A veut dire que la variable A est vraie et
vaut 1. nA veut dire que la variable A est fausse et vaut
0. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Simplification
Elle
est égale à 1 pour A = 1 quelle que soit la valeur de B, C et D Soit Fg = A
Elle
est égale à 1 pour nD = 1 quelle que soit la valeur de A, B et C Soit Fl = nD
lorsque
Fg est à 1 ou bien lorsque
Fl est à 1 ou encore si
les deux sont à 1 F = Fg + Fl F = A + nD Cette
expression toute simple est égale à celle de la liste des douze termes
ci-dessus |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Trouver la composition de ma bibliothèque, sachant que
j’ai:
Diagramme
de Karnaugh
Introduction
des données
Déductions
Bilan
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Anecdote: une sévère
leçon pour débutant!
|
Alors
jeune ingénieur, concepteur de systèmes logiques, et tout imbu de cette belle
théorie de l'optimisation avec diagrammes de Karnaugh, je récupère le fruit
de mes cogitations. Un magnifique panier (rack) de cartes électroniques juste
sorti de production. Avec
mes collaborateurs, nous entamons la mise au point. En ce temps-là (fin des
années 1960, les tous débuts des circuits logiques intégrés), les
oscilloscopes n'avaient que deux sondes (pas encore d'analyseurs logiques
multi-traces). L'optimisation
m'avait conduit à coder tous les états du système sur les combinaisons de
huit bits. Mais, problème! Impossible de les observer avec deux sondes
seulement. J'ai dû revoir mes circuits pour isoler les états du système sur
un seul bit. L'optimisation aux oubliettes. La mise au point fut possible et
le système vite admis en service opérationnel. |
|
|
||
|
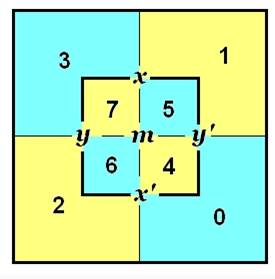
Lewis Carroll
utilisait des diagrammes de cette sorte pour résoudre ses énigmes (proches
des tableaux de Karnaugh ou des diagrammes de Venn). En haut, cas de deux
variables. Celles-ci sont notées dans le tableau. En bas, cas de trois
variables. 9a se complique un peu. Ces diagrammes pouvaient même être ternaires. Par exemple:
Lewis Carroll utilisait ces diagrammes surtout à
des fins pédagogiques. Il a écrit un livre intitulé "The Game of
Logic" destiné à enseigner la logique aux enfants. |
|
|
Voir le site en anglais:
The
Logic Diagrams Of Lewis Carroll
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()