|
|||||||||||||||||||||||||||||||||||
![]()
|
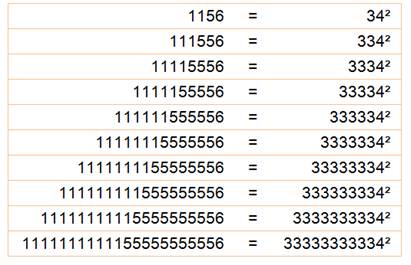
Motifs répétitifs avec des carrés Croissance
cristalline des chiffres de certains carrés. Exemple typique:
|
Formes en ABB..BBC et carrés ou cubes
|
Exemple
avec 266..667 => Carrés des formes ABB..BBC Formes itératives pour B multiple de 3 quels que soient les valeurs de
A et C. Cubes des formes ABB..BBC Formes itératives pour B = 0 ou 9 quels que soient les valeurs de A et
C. |
|
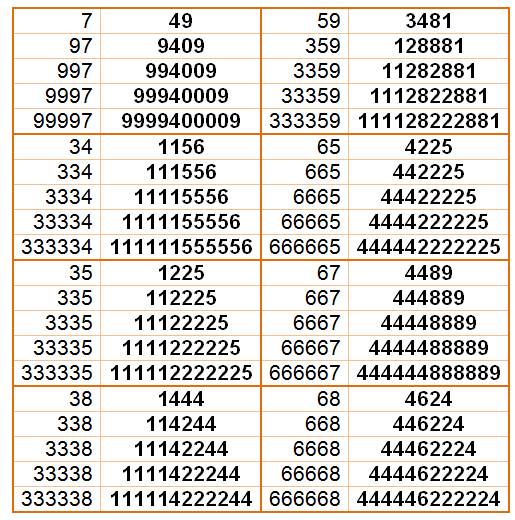
Voir Tables complètes
![]()
|
|
|
|
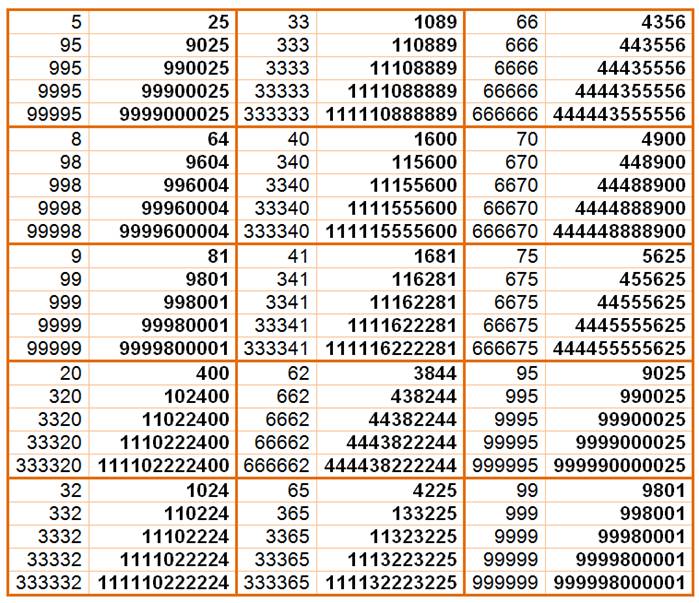
Le carré de 99 997 est 9 999 400 009, un motif qui
croit sans cesse lorsqu'on ajoute des 9 à gauche. Ce motif comporte pas plus
de 3 chiffres différents.
|
|
|
|
|
|
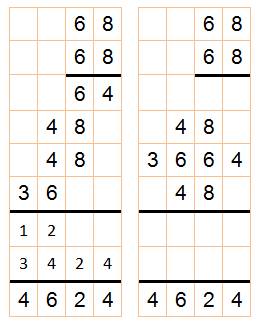
Exemple de développement
jusqu'à 20 itérations:
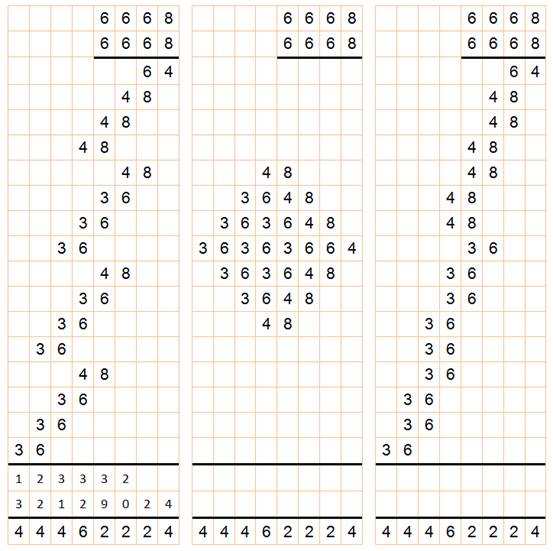
Multiplication
posées pour 68, 668 et 6668 chiffres
Les petits chiffres en bas montrent la somme en
dizaines en haut et en unités en bas.
La présentation centrale, regroupant des chiffres
disjoints, est esthétique, mais n'apporte pas grand-chose à l'explication de
pourquoi ça marche avec 68 et moins bien avec d'autres nombres. |
|
|
|
||
|
Nombres en aaa …ab au carré et le développement
de la forme générique. Les coefficients paraissent effectivement propices à des
motifs esthétiques, mais ne le démontrent pas. Seule l'exploration révèle les meilleures
configurations. |
(10a+ b)² = 100a² + 20ab + b² |
|
|
(100a + 10a + b)² = (110a
+ b)² = 12100a² + 220ab + b² |
||
|
(1000a + 100a + 10a + b)²
= (1110a + b)² = 1232100a² + 2220ab + b² |
||
|
(10000a + 1000a + 100a +
10a + b)² = (11110a + b)² = 123432100a² + 22220ab + b² |
||
|
Quantité
d'autres nombres conduisent à des motifs itératifs infinis. Les nombres en 333…b,
666…b et 999…b sont très généreux, mais plus de 4 chiffres différents
apparaissent dans les résultats. |
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Iteration/aMOTIF/Criscarr.htm |
![]()