|
Édition du: 30/01/2022 |
|
INDEX |
Énigmes – Trajets |
|||
![]()
|
Bicyclette – Sens de parcours selon la trace Une énigme
résolue par Sherlock Holmes dans un des romans de Conan Doyle (1859-1930). Comment
deviner le sens de marche d'une bicyclette par l'observation de la trace de
ses roues ? |
||
|
|
Sommaire de cette page >>> L'énigme >>> La géométrie des traces >>> Impossible à deviner >>> Historique |
Débutants Glossaire |
|
La
situation Vous arrivez sur la scène du crime. Le voleur de bijoux vient de
s'enfuir à vélo. Les traces des roues de sa bicyclette sont encore bien
visibles. Dans quelle direction est-il parti ? |
Contrairement à Sherlock, vous ne pouvez compter
que sur la géométrie des deux traces de roue. Pas question de prendre pour indice la différence
de profondeur des marques due au poids sur la roue arrière. |
|
|
La
roue avant Une première observation simple, vous permettra de déterminer quelle
est la trace de la roue avant. C'est celle qui dessine les courbes de plus grande amplitude. Mais cela ne dit rien sur le sens. |
La roue avant décrit la courbe la plus ondulée. |
|
|
La
roue arrière En ligne droite comme en virage, la structure rigide du vélo maintient
la roue arrière dans la direction du point de contact de la roue avant. Ce qui se
traduit sur la courbe par: la tangente (verte) à la courbe
"arrière" (rouge) coupe la courbe "avant" (bleue) là où
se trouve la roue avant. Oui, mais: la
tangente en A coupe la courbe bleue en deux points P et Q. Notre remarque
est pertinente mais pas suffisante pour déterminer le sens de roulage du
vélo. |
La roue avant se trouve sur la tangente à la courbe suivie par la roue arrière (rouge). |
|
|
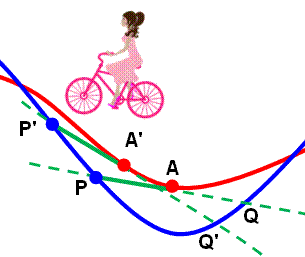
Les
deux roues La distance entre la roue avant et la roue arrière est constante. Alors, pour lever
le doute, dessinons deux tangentes et observons les distances. Comparons les
longueurs de vélo (entre points de contact des roues): AP = A'P' alors
que AQ est plus petit que A'Q'. L'égalité
traduit la conservation de la longueur du vélo. Le vélo se dirige
vers les P, donc vers la gauche. En prime, nous
avons aussi la taille du vélo. |
La roue avant se trouve du côté: AP = constante. |
|
|
Dans le
cas où le cycliste suit une trajectoire parfaitement rectiligne, impossible
de déterminer le sens. Les deux pistes
sont confondues. |
|
||
|
Si le
cycliste dessine un rond parfait, impossible de déterminer le sens. Les distances
(r) sont égales de part et d'autre des tangentes. Note: L'aire
séparant les deux traces d'un vélo décrivant un cercle parfait ou même une
courbe convexe quelconque vaut Le rayon r est alors la distance
entre les deux points de contact des roues. Voir Aire
de la couronne |
|
||
|
1904
– Sherlock Holmes The Adventure of the Priory School
Sir Arthur Conan Doyle – 1904 L'École du Prieuré en français Holmes
et Watson partent inspecter la lande. Outre des traces de pas de vache qui
n'ont pas d'intérêt, ils y trouvent la trace de
pneu de la bicyclette de Heidegger. En suivant cette trace, ils
finissent par découvrir, caché derrière un bosquet, le corps sans vie du
professeur avec une importante blessure au front. Source Wikipédia |
|
|
|
-
This track, as you perceive, was made by a rider who was
going from the direction of the school. -
Or towards it ? -
No, no, my dear Watson. The more deeply sunk impression is,
of course, the hind wheel, upon which the weight rests. (…) It was
undoubtedly heading away from the school. |
-
Cette trace, comme vous le voyez, a été faite par un
cycliste qui venait de la direction de l'école. -
Ou vers elle? -
Non, non, mon cher Watson. La marque la plus profonde est,
bien sûr, la roue arrière, sur laquelle repose le poids. (…) Il s'éloignait
sans aucun doute de l'école. |
|
|
Années
1980 |
Université
de Princeton, ce problème apparait dans un cours de géométrie. |
|
1996 |
Which Way
did the Bicycle Go? ... and Other Intriguing Mathematical Mysteries par
Joseph Konhauser, Dan Velleman, et Stan Wagon |
|
2002 |
Can
a Bicycle Create a Unicycle Track? – David L. Finn Il démontre qu'il est possible de créer une
courbe unique suivie par les deux roues sans que la trajectoire soit
rectiligne. Calcul avancé avec équations différentielles. |
Livre pour enfant de Christine Naumann-Villemin
Editions Kaléidoscope – 2019

Voir Patronyme
Villemin
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |