NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 09/07/2017 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Dénombrement
Débutants Dénombrement	Autour d'une TABLE RONDE				Glossaire Combinatoire
INDEX Dénombrement	Introduction	Position (énigme)	Voisins différents	Couples différents
		3 personnes	4 personnes	5 personnes
		Sommaire de cette page

Autour de la TABLE

Places assises

Jamais le même voisin

Parmi toutes les permutations de personnes autour d'une table ronde quels sont celles telles qu'une personne ne retrouve jamais la même personne à côté de lui.

C'est le défi le plus connu concernant la disposition autour des tables rondes. La solution passe par la constitution de graphes hamiltoniens. Curieusement la question de savoir s'il existe un chemin hamiltonien et, si oui, combien, n'est pas résolue.

Anglais: Seating arrangement problem / Around table arrangements / Hamiltonian Circuit

Trois personnes
Il n'existe qu'une seule possibilité pour disposer trois personnes autour d'une table. On peut bien entendu inverse 2 et 3, mais les voisinages seront les mêmes. Le circuit hamiltonien est unique avec le triangle. La quantité est également égale à: Q3 = ½ (n – 1)(n – 2) = ½ (2 x 1) = 1

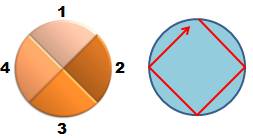
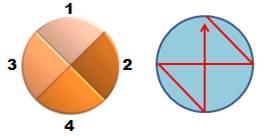
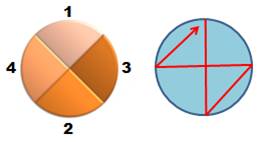
Quatre personnes
Il n'existe qu'une seule possibilité pour disposer trois personnes autour d'une table. On peut bien entendu inverse 2 et 3, mais les voisinages seront les mêmes. Le circuit hamiltonien est unique avec le triangle. La quantité est également égale à: Q3 = ½ (n – 1)(n – 2) = ½ (2 x 1) = 1

Cas de 7 personnes autour d'une table ronde
· The

Suite	Quatre autour de la table Rondes sociales
Voir	Combinatoire – Panorama Combinatoire
Aussi	Dénombrer – Index Compter Énigmes – Index Énigmes sur les familles
Cette page	http://villemin.gerard.free.fr/Denombre/aaaTable/Voisin.htm