|
||||||||||||||||||||||||||||
![]()
|
TYPES
DE SITUATIONS en
dénombrement classique Une visite introductive aux 4 types de situations classiques. Une synthèse en tableau est disponible en Panorama d'un coup d'œil. Où il est question d'ordre ou pas et
de répétitions ou pas. |
|
|
|||
|
Soit 1 jeton
rouge et 1 jeton vert Combien de façons de les disposer en ligne
devant moi? |
O O O O |
2 |
|
|
Soit 3 jetons
de couleurs Combien de façons de les disposer?
Ma liste de comporte alors 3 x 2 x 1 = 6 dispositions. |
O O O O O O O O O O O O O O O O O O |
6 |
|
|
Attention, on change de jeu ! |
|
|
|
|
Soit des
jetons de 2 couleurs sur 3 cases Combien de façons de les disposer sur trois
cases?
Soit
le bilan: 2 x 2 x 2 = 23 = 8
dispositions |
|
8 |
|
|
|
||
|
Soit un
compteur binaire à 3 positions Ce compteur peut montrer l'une des deux
positions binaires 0 ou 1. Combien de façons de disposer ces chiffres
sur trois cases?
Soit
un bilan: 2 x 2 x 2 = 8 = 23
dispositions |
|
8 |
|
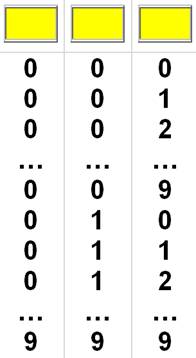
Soit un
compteur numérique à 3 positions Chaque case peut recevoir chacun des
chiffres indépendamment des cases voisines.
Soit un bilan: 10
x 10 x 10 = 1000 = 103 dispositions |
|
8 |
|
|
||
|
Soit un
compteur à 2 positions et 3 lettres Soit les lettres a, b et c. Combien de façons de disposer ces lettres
sur trois cases?
Soit un bilan: 3
x 3 = 9 = 32 dispositions |
|
9 |
|
|
||
|
Avec les exemples précédents, on note le
mode de calcul:
On observe ab et ba existent
séparément:
Il s'agit de compteurs dont chaque case
peut prendre n'importe quelle valeur, y compris celle de la case voisine
Il s'agit d'un arrangement à
répétitions qui s'appelle une liste
ou p-liste ou p-uplet (comme dans
doublet ou triplet). Autres
exemples
|
Arrangement
à répétitions
|
|
|
|
|
|
BILAN
COMPLET Les quatre situations classiques en analyse
combinatoire se distinguent selon que les éléments sont:
Les
quatre situations
1 Cette rangée donne
les p-arrangements; cependant le terme Arrangement désigne de manière
classique un arrangement sans répétition 2 Cette rangée donne
les p-combinaisons; cependant le terme Combinaison désigne de manière
classique une combinaison sans répétition 3 Une p-liste est le
terme moderne pour arrangement avec répétitions 4 Pas de nom bien
clair pour cette combinaison à répétitions 5 Une permutation
est un arrangement complet de n objets parmi n Formules
Exemples
avec 2 parmi trois éléments de {a, b, c}
|
|
![]()
|
Suite |
|
|
Rappel |
|
|
Voir |
|
|
|
![]()