|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Autour
de la TABLE Places
assises Il existe de nombreux jeux
de placement autour d'une table. Des énigmes plus ou moins difficiles. Les plus simples consistent
à découvrir qui est placé à telle ou telle place en fonction d'indices. Les plus classiques
consistent à trouver toutes les possibilités de placements en toute liberté
ou en positionnant certaines personnes à certaines places. |
Anglais: Seating arrangement problem / Around
table arrangements
|
Cinq
places numérotées de 1 à 5 pour cinq personnes nommées de 1 à 5. Le premier
choisit une place au hasard. Les suivants prennent leur place ou choisisse
une place au hasard si celle-ci est déjà occupée. Quelle est la probabilité
que le cinquième trouve sa place ? |
|
|
||
|
Avec une table en long (ou banc) On écrit
toutes les possibilités et, on en compte six. On peut
raisonner comme suit:
Soit
trois fois deux possibilités: QB = 3 x 2 = 6 |
Disposition
Toutes les possibilités 1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1 |
|
|
Avec
quatre personnes on aurait: |
4 possibilités pour placer le 1er, 3 possibilités pour placer le 2e, 2 possibilités pour placer le 3e, et 1 possibilités pour placer le4e. Les opératons étant successives, le principe
multiplicatif s'applique Q = 4 x 3 x 2 x 1 = 4 ! = 24 |
|
|
Avec n
personnes on aurait: |
Q = n! |
|
Voir Trois sur un banc et approche
des factorielles
|
|
||
|
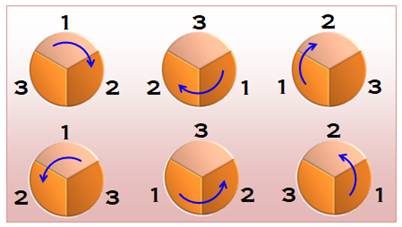
Avec une table ronde (ou en cercle) Dans ce
cas, il existe aussi six dispositions. Mais observez que les dispositions sur
une ligne sont identiques en les faisant pivoter d'un tiers de tour. Il reste
dont deux configurations: les deux de gauche, en plaçant, par exemple, le 1
en haut. QC = 2 |
Toutes les possibilités
Les deux dispositions sur une colonne sont identiques au sens de la
rotation près. |
|
|
Avec
quatre personnes on aurait: |
Raisonnement n°1 Toutes les possibilités comme avec une table en long: QL = 4 x 3 x 2 x 1 = 4 ! = 24 Mais, la table étant ronde, chacune des dispositions se reproduit avec
le même voisinage tout les quarts de tour. QR = 24 / 4 = 6 Raisonnement n°2 On place le premier n'importe où autour de la table. 3 possibilités pour placer le 2e, 2 possibilités pour placer le 3e, et 1 possibilités pour placer le4e. QR = 3 x 2 x 1 = 3! = 6 |
|
|
Avec n
personnes on aurait: |
Q = n! / n = (n-1)! |
|
Voir Trois sur un banc et approche
des factorielles
En résumé: toutes les permutations possibles sans contrainte
|
Table en long La quantité de
permutations de n personnes est égale à n! Exemples: 3 personnes: 6 6 personnes: 720 |
Table en cercle La quantité de
permutations de n personnes est égale à
(n – 1)! Exemples: 3 personnes: 2 6 personnes: 120 |
Voir Permutations
![]()
|
Disposer
les convives autour de la table est un problème classique de dénombrement.
Les énigmes de places assises autour d'une table introduisent des contraintes
qui rendent beaucoup plus difficile la recherche des dispositions
acceptables: jamais le même voisin, jamais le même couple de voisins, avec
autant de déjeuners que possibles, seulement un deuxième déjeuner, etc. |
|
|
||
|
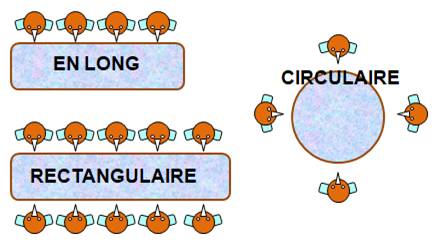
Types de table Les trois types
principaux:
|
|
|
|
Disposition des convives
individuels Combien de repas
peut-on organiser |
En
plaçant les personnes dans toutes les configurations possibles ? De
façon que personne ne retrouve le même voisin? De
façon que personne ne retrouve le même couple?
– Dudeney (1905) – Problème résolu pour n pair et que jusqu'à n = 41 pour n
impair (no person shall ever have the same two
neighbours twice). |
|
|
Combien de deuxième
repas existe-t-il |
De
façon que personne ne retrouve le même voisin? De
façon que personne ne retrouve le même couple? |
|
|
Disposition de couples Combien de repas peut-on
organiser |
De
façon à alterner hommes et femmes et à ne placer personne à côté de son (ou
sa) conjoint(e)? Problème
dit des ménages – Édouard Lucas (1891). |
|
|
Disposition entre amis Est-il possible de positionner
les participants entre deux personnes connues. |
Vingt
personnes sont autour d'une table ronde. Chacune connait au moins dix des
participants. Montrer
qu'il existe une disposition telle que chacun est situé entre deux personnes
connues. |
|
|
Énigme Cinq
places numérotées de 1 à 5 pour cinq personnes nommées de 1 à 5. Le premier
choisit une place au hasard. Les suivants prennent leur place ou choisisse
une place au hasard si celle-ci est déjà occupée. Quelle est la probabilité
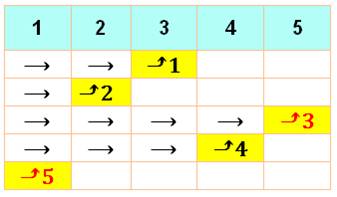
que le cinquième trouve sa place ? Solution avec un exemple
En
fin de compte, au moment où il doit rejoindre sa place, le 5 va à sa place ou
à la seule place libre. Il a donc une chance sur
deux de se retrouver à sa place. |
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
![]()