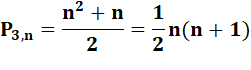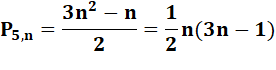|
Édition du: 15/07/2022 |
|
INDEX |
Nombres polygonaux – Tables |
|||
![]()
|
Table des NOMBRES POLYGONAUX |
||
|
|
Sommaire de cette page >>> Formules >>> Table des nombres POLYGONAUX >>> Racines numériques des nombres polygonaux |
Débutants Nombres figurés
ou géométriques Glossaire |
Retour Nombres polygonaux
|
Triangulaires |
|
|
|
Carrés |
|
|
|
Pentagonaux |
|
|
|
Hexagonaux |
|
|
|
Heptagonaux |
|
|
|
k-gonaux |
|
|
|
|
||
|
En jaune, le principe de
construction: les polygonaux d'ordre 5 (exemple) sont tous en progression
arithmétique (25 – 15 = 10) dont la raison est égale au nombre triangulaire
(10) d'ordre juste inférieur. Note: voir Tables semblables mais croisées >>> |
|
Nom |
Formule avec n => |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Tri |
½ n ( n + 1) |
1 |
3 |
6 |
10 |
15 |
21 |
28 |
36 |
45 |
55 |
|
C |
½ n ( 2 n - 0) |
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
81 |
100 |
|
Pent |
½ n ( 3 n - 1) |
1 |
5 |
12 |
22 |
35 |
51 |
70 |
92 |
117 |
145 |
|
Hex |
½ n ( 4 n - 2) |
1 |
6 |
15 |
28 |
45 |
66 |
91 |
120 |
153 |
190 |
|
Hept |
½ n ( 5 n - 3) |
1 |
7 |
18 |
34 |
55 |
81 |
112 |
148 |
189 |
235 |
|
Octogon |
½ n ( 6 n - 4) |
1 |
8 |
21 |
40 |
65 |
96 |
133 |
176 |
225 |
280 |
|
Enné Non |
½ n ( 7 n - 5) |
1 |
9 |
24 |
46 |
75 |
111 |
154 |
204 |
261 |
325 |
|
Décagonal |
½ n ( 8 n - 6) |
1 |
10 |
27 |
52 |
85 |
126 |
175 |
232 |
297 |
370 |
|
11-gon Hendécagonal |
½ n ( 9 n - 7) |
1 |
11 |
30 |
58 |
95 |
141 |
196 |
260 |
333 |
415 |
|
12-gon Dodéc |
½ n (10 n - 8) |
1 |
12 |
33 |
64 |
105 |
156 |
217 |
288 |
369 |
460 |
|
13-gon |
½ n (11 n - 9) |
1 |
13 |
36 |
70 |
115 |
171 |
238 |
316 |
405 |
505 |
|
14-gon |
½ n (12 n - 10) |
1 |
14 |
39 |
76 |
125 |
186 |
259 |
344 |
441 |
550 |
|
15-gon |
½ n (13 n - 11) |
1 |
15 |
42 |
82 |
135 |
201 |
280 |
372 |
477 |
595 |
|
16-gon |
½ n (14 n - 12) |
1 |
16 |
45 |
88 |
145 |
216 |
301 |
400 |
513 |
640 |
|
17-gon |
½ n (15 n - 13) |
1 |
17 |
48 |
94 |
155 |
231 |
322 |
428 |
549 |
685 |
|
18-gon |
½ n (16 n - 14) |
1 |
18 |
51 |
100 |
165 |
246 |
343 |
456 |
585 |
730 |
|
19-gon |
½ n (17 n - 15) |
1 |
19 |
54 |
106 |
175 |
261 |
364 |
484 |
621 |
775 |
|
20-gon Icos |
½ n (18 n - 16) |
1 |
20 |
57 |
112 |
185 |
276 |
385 |
512 |
657 |
820 |
|
21-gon |
½ n (19 n - 17) |
1 |
21 |
60 |
118 |
195 |
291 |
406 |
540 |
693 |
865 |
|
22-gon |
½ n (20 n - 18) |
1 |
22 |
63 |
124 |
205 |
306 |
427 |
568 |
729 |
910 |
|
23-gon |
½ n (21 n - 19) |
1 |
23 |
66 |
130 |
215 |
321 |
448 |
596 |
765 |
955 |
|
24-gon |
½ n (22 n - 20) |
1 |
24 |
69 |
136 |
225 |
336 |
469 |
624 |
801 |
1 000 |
|
25-gon |
½ n (23 n - 21) |
1 |
25 |
72 |
142 |
235 |
351 |
490 |
652 |
837 |
1 045 |
Suite pour n de 11 à 20
|
Nom |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
Tri |
66 |
78 |
91 |
105 |
120 |
136 |
153 |
171 |
190 |
210 |
|
C |
121 |
144 |
169 |
196 |
225 |
256 |
289 |
324 |
361 |
400 |
|
Pent |
176 |
210 |
247 |
287 |
330 |
376 |
425 |
477 |
532 |
590 |
|
Hex |
231 |
276 |
325 |
378 |
435 |
496 |
561 |
630 |
703 |
780 |
|
Hept |
286 |
342 |
403 |
469 |
540 |
616 |
697 |
783 |
874 |
970 |
|
Octogon |
341 |
408 |
481 |
560 |
645 |
736 |
833 |
936 |
1 045 |
1 160 |
|
Enné Non |
396 |
474 |
559 |
651 |
750 |
856 |
969 |
1 089 |
1 216 |
1 350 |
|
Dec |
451 |
540 |
637 |
742 |
855 |
976 |
1 105 |
1 242 |
1 387 |
1 540 |
|
11-gon Hendec |
506 |
606 |
715 |
833 |
960 |
1 096 |
1 241 |
1 395 |
1 558 |
1 730 |
|
12-gon Dodéc |
561 |
672 |
793 |
924 |
1 065 |
1 216 |
1 377 |
1 548 |
1 729 |
1 920 |
|
13-gon |
616 |
738 |
871 |
1 015 |
1 170 |
1 336 |
1 513 |
1 701 |
1 900 |
2 110 |
|
14-gon |
671 |
804 |
949 |
1 106 |
1 275 |
1 456 |
1 649 |
1 854 |
2 071 |
2 300 |
|
15-gon |
726 |
870 |
1 027 |
1 197 |
1 380 |
1 576 |
1 785 |
2 007 |
2 242 |
2 490 |
|
16-gon |
781 |
936 |
1 105 |
1 288 |
1 485 |
1 696 |
1 921 |
2 160 |
2 413 |
2 680 |
|
17-gon |
836 |
1 002 |
1 183 |
1 379 |
1 590 |
1 816 |
2 057 |
2 313 |
2 584 |
2 870 |
|
18-gon |
891 |
1 068 |
1 261 |
1 470 |
1 695 |
1 936 |
2 193 |
2 466 |
2 755 |
3 060 |
|
19-gon |
946 |
1 134 |
1 339 |
1 561 |
1 800 |
2 056 |
2 329 |
2 619 |
2 926 |
3 250 |
|
20-gon Icos |
1 001 |
1 200 |
1 417 |
1 652 |
1 905 |
2 176 |
2 465 |
2 772 |
3 097 |
3 440 |
|
21-gon |
1 056 |
1 266 |
1 495 |
1 743 |
2 010 |
2 296 |
2 601 |
2 925 |
3 268 |
3 630 |
|
22-gon |
1 111 |
1 332 |
1 573 |
1 834 |
2 115 |
2 416 |
2 737 |
3 078 |
3 439 |
3 820 |
|
23-gon |
1 166 |
1 398 |
1 651 |
1 925 |
2 220 |
2 536 |
2 873 |
3 231 |
3 610 |
4 010 |
|
24-gon |
1 221 |
1 464 |
1 729 |
2 016 |
2 325 |
2 656 |
3 009 |
3 384 |
3 781 |
4 200 |
|
25-gon |
1 276 |
1 530 |
1 807 |
2 107 |
2 430 |
2 776 |
3 145 |
3 537 |
3 952 |
4 390 |
Suite pour n de 21 à 30
|
|
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
|
Tri |
231 |
253 |
276 |
300 |
325 |
351 |
378 |
406 |
435 |
465 |
|
C |
441 |
484 |
529 |
576 |
625 |
676 |
729 |
784 |
841 |
900 |
|
Pent |
651 |
715 |
782 |
852 |
925 |
1001 |
1080 |
1162 |
1247 |
1335 |
|
Hex |
861 |
946 |
1035 |
1128 |
1225 |
1326 |
1431 |
1540 |
1653 |
1770 |
|
Hept |
1071 |
1177 |
1288 |
1404 |
1525 |
1651 |
1782 |
1918 |
2059 |
2205 |
|
Octogon |
1281 |
1408 |
1541 |
1680 |
1825 |
1976 |
2133 |
2296 |
2465 |
2640 |
|
Ennéagonal / Nonagonal |
1491 |
1639 |
1794 |
1956 |
2125 |
2301 |
2484 |
2674 |
2871 |
3075 |
|
Dec |
1701 |
1870 |
2047 |
2232 |
2425 |
2626 |
2835 |
3052 |
3277 |
3510 |
|
|
|||
|
La racine
numérique est la somme des chiffres (comme pour la preuve par 9). Les racines numériques des polygonaux obéissent à un cycle régulier
très souvent de longueur 9 (Tableau). Le tableau est lui-même cyclique: les dodécagonaux ont le même cycle
que les triangulaires et ainsi de suite (Tableau bleu ci-dessous). |
|
||
|
Programme Maple: racine numérique des nombres
polygonaux
|
Commentaires Deux procédures: calcul du nombre polygonal et
calcul de la racine
numérique. Le programme principal boucle sur k de 3 à 15. Il
commence par initialiser une liste L. Puis, il lance une boucle en n de 1 à 20; calcule
le polygonal (k, n), sa racine numérique rn et loge celle-ci dans la liste L. À chaque fin de boucle en n, le programme édite
la liste des racines pour une valeur de k. Copie du résultat ci-dessous.
|
||
Voir Programmation – Index
![]()
|
Retour |
|||||||||||||||||||||
|
Suite |
|
||||||||||||||||||||
|
Voir |
|
||||||||||||||||||||
|
Site |
|
||||||||||||||||||||
|
OEIS |
Suite en
proposant la liste des premiers nombres |
||||||||||||||||||||
|
Cette page |