|
|||||||||||||||||||||||||||||||||||
![]()
|
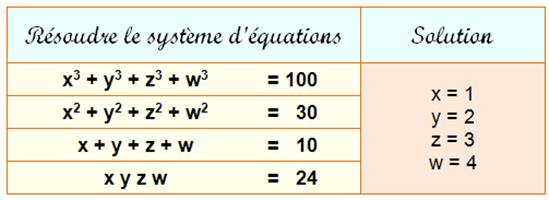
SYSTÈMES d'ÉQUATIONS en 100 Vers l'an 900, Abu Kamil publie un livre dans lequel, pour la première fois,
on compte la quantité de solutions à un problème.
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Programme
Notes: les plages d'exploration (a de 20 à 40, par exemple) correspondent à l'essai dont les résultats sont
présentés ci-dessous. Le programme donne toutes les solutions, même celles
avec des termes fractionnaires. Le
début du tableau des solutions
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Statistiques sur cette
plage de calcul |
|
||||||||||||||||||||||||||||||
YF
nombre total d'occurrences. YE
nombre d'occurrences non fractionnaires. |
|||||||||||||||||||||||||||||||
|
Temps de calcul |
|
||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
a MAXIMUM
a MINIMUN
On
retiendra
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
|
PLAGE de CALCUL pour c, d
et e |
|
||||||||||||||||||||||||||||||||||||||||||
|
Plage
pour c
Plage
pour d
Plage
pour e
Bilan
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
|
YF
nombre d'occurrences total YE
nombre d'occurrences valides (pas de fractions)
|
|||||||||||||||||||||||||||||||
![]()
|
Suite |
|
|
Voir |
![]()