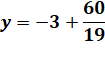|
|||||||||||||||||||||||||||||||||||||
![]()
|
SYSTÈME D'ÉQUATIONS |
|
|
Deux
équations pour déterminer la valeur de deux
inconnues. Trois
équations pour déterminer la valeur de trois
inconnues. … Finalement, ce n'est pas si
compliqué, avec de la méthode et de la rigueur.
|
Résolution muette
|
Anglais:
Simultaneous equations, system of equations
|
Arthur
achète un litre de lait et un litre d'eau pour 5 euros. Bernard
achète un litre d'eau et un litre de soda pour 7 euros. Camille
achète un litre de lait et un litre se soda pour 4 euros. Si
Danièle achète un litre de lait, un litre d'eau et un litre de soda, combien
va-t-elle payer? |
|
|
||
|
Pour
rétablir l'équilibre il faut une masse de 1 à droite.
Il vous paraît déjà évident que Y vaut 1.
Cela
sera utile pour les cas plus complexes
|
|
|
|
Commentaires et bilan |
|
|
Remarque
Astuce
Obtenir deux équations avec la
même quantité de x. |
|
|
Des
personnes se trouvent dans deux pièces A et B. Si
l'un de A va dans B, alors ils y seront deux fois plus nombreux. Si
l'une de B va dans A, alors ils seront à égalité. Combien
de personnes dans chaque pièce? |
|
|
||
|
Énigme plus subtile qu'il n'y
parait On donne le poids pour certaines combinaisons de
ces trois objets. On demande le poids de ces trois objets réunis. Solution J'ai fait de l'algèbre, alors je mets en
équations avec trois inconnues … Oups, il ya beaucoup plus simple. En ajoutant les trois pesées, on obtient: Le poids pour un
seul de chaque est: 120 / 2 = 60 kg. Résolution
|
Quel est le poids des trois objets
réunis ?
Leçon Attention à bien lire l'énoncé: on demande le
poids des trois et non de chacun. Un petit temps de réflexion supplémentaire,
évitera de se lancer dans un calcul algébrique. |
|
Voir Brève
899 / Énigmes
de pesées
|
|
||
|
On compte
Dire
combien de billets de chaque (d et v?). |
Q = 1 500 S = 25 000 euros |
|
|
Résolution d'un système
d'équation Mise en
équation: |
d + v =
1 500 10d + 20v = 25 000 |
|
|
Réécriture
en prenant 20 fois la première: |
20d + 20v = 30 000 10d + 20v = 25 000 |
|
|
Soustraction: |
10d + 0 = 5 000 d = 500 |
|
|
Calcul de
v: |
d + v = 1 500 500 + v = 1 500 v = 1 000 |
|
|
Interprétation
sans les équations Construction du
graphique La droite
rouge indique une quantité de billets égale à 1 500.
Nous
cherchons le point sur cette droite pour lequel la somme est situé entre ces
deux valeurs, et plus précisément 25 000.
Opérations 1)
L'écart 25 000 – 15 000 = 10 000 doit être
comblé en échangeant un billet de dix contre un billet de vingt. Pour chaque
échange, la somme grimpe de 20 – 10 = 10 euros 2) Pour
combler les 10 000 euros, il faut effectuer 10 000 /
10 = 1000 tels échanges Le point sur la droite se trouve en (d = 500 et v = 1000). |
||
Voir Méthode
de la fausse position
|
CAS PRATIQUE: RÈGLE DE LA TÊTE ou
méthode par élimination |
|
||
|
|
{ |
2x + 3y x
+ y |
= 40 = 15 |
|
Nous
n'avons toujours les deux inconnues en piste.
|
|
x +
2y |
= 25 |
|
Pour obtenir 2x
sur la deuxième, multiplions les deux membres par 2 (règle des paquets). |
{ |
2x + 3y 2(x + y) |
= 40 = 2 x15 |
|
En
calculant les produits. |
{ |
2x + 3y 2x + 2y |
= 40 = 30 |
|
Nous
pouvons effectuer la soustraction.
|
|
0 + y |
= 10 |
|
Pour calculer x, reprenez l'équation de départ x
+ y = 15 En remplaçant y par 10, vous trouvez x
= 5 |
{ |
y x |
= 10 = 5 |
|
Commentaires et bilan |
|
|
Par multiplication des
membres de l'équation, obtenir la même tête
sur les deux équations pour permettre l'élimination de cette tête lors d'une soustraction. Principe imagé
On baptise "reste"
toute la partie de l'équation qui ne dépend pas de x.
Note Si
cela est plus pratique, il est possible de faire la même démarche avec les
coefficients de y ou de pratiquer une addition plutôt qu'une soustraction. |
|
Amusement
|
|
||
|
Problème
|
Mise en équation
(A) (B) (C) Réponse x = 10 + 3 + 1 = 14 |
|
|
Remarques Il est incontestable que l'image montre volontairement (pour piéger!)
un régime de quatre bananes et, sur la dernière ligne, seulement trois. Quant aux noix de coco, ce sont clairement des moitiés de noix. |
Les trois premières lignes montrent trois équations comportant trois
inconnues. Donc, système simple à résoudre. La seule précaution fut simplement dans le fait de nommer la banane
(et non le régime) et c la moitié de noix de coco pour ne pas s'embêter avec
des ½ dans les calculs. |
|
|
|
Autre énigme vue sur Internet en juin 2016. Sans difficulté
particulière, sauf un piège avec la quantité de pétales sur la fleur bleue. Résolution 3 rouges = 60 => 1 rouge =
20 1 rouge (20) + 2 bleues = 30 => bleue à 5 pétales = ½ (30-20) = 5.
Soit un pétale bleu = 1. 1 bleue cinq pétales (5) – 2 jaunes = 3 => une jaune = ½
(5 – 3) = 1 1 jaune (1) + 1 rouge (20) x 1 bleue quatre pétales (4 x 1) = 1 + 20 x
4 = 81. |
|
Les vingt fioles |
||
|
Énigme Toutes
ces fioles sont sur trois étagères. Le poids total est 8,4 kg, et il est
également réparti sur les trois niveaux. Quel
est le poids de chaque fiole ? Difficulté Aucune:
il s'agit de résoudre un système d'équation très simple. |
|
|
|
Solution On
note G, M et P les grosses, moyennes et petites fioles. Les
trois premières équations témoignent du même poids sur chaque étagère: 8,4 /
3 = 2, 8 kg. résolution
en |
|
|
D'après Science
et Vie
Voir Autres
problèmes qui affolent le Net … / Énigmes
|
|
|||
|
|
{ |
5x + 3y 2x +
y |
= 1 = 3 |
|
|
{ |
2 (5x + 3y) 5 (2x +
y) |
= 2 x 1 = 5 x 3 |
|
|
{ |
10x + 6y 10x + 5y |
= 2 = 15 |
|
|
|
0 + y |
=
–13 |
|
|
|
2x
+ y 2x
+ (–13) 2x x |
= 3 = 3 = 16 = 8 |
|
|
{ |
5 . 8 + 3 . (–13) 2 . 8 +
(–13) |
= 1 = 3 |
|
Apprenez
à noter proprement les équations en alignant les termes de même nature. Une erreur
est si vite arrivée ! Pour finir, toujours vérifier. |
|
|
||
|
Résoudre ce système de deux
équations à deux inconnues. |
4x + 5y + 150 = 0 36x + 9y + 9 = 0 |
|
|
1) Je peux multiplier les
deux membres de l'égalité par le même nombre sans changer l'égalité. 2) En multipliant la
première par 9 et la seconde par 5, nous aurons la même quantité de y dans
les deux équations. |
9 ( 4x + 5y + 150) = 0 5 (36x + 9y + 9) = 0 |
|
|
On effectue les
multiplications |
36x + 45y + 1350 = 0 180x + 45y + 45 = 0 |
|
|
Soustraction des égalités |
–144x + 0y + 1305 = 0 |
|
|
Calcul de x en retranchant 1305
de chaque côté, puis en divisant par 144 de chaque côté |
–144x = – 1305 x = –1305 / (–144) = 9,0625 |
|
|
Calcul de y en reprenant
l'une des équations (n'importe laquelle) |
4*9,0625 + 5y + 150 = 0 5y = –150 – 36,25 = –186,25 y = –186,25 / 5 = –37,25 |
|
|
On vérifie avec la seconde
équation |
36x + 9y + 9 = 0 36 * 9,0625 + 9 * (–37,25) +
9 = 326,25 – 335,25 +9 = 0 |
|
|
Problème Résoudre
ce problème d'arrosage. Pas si simple sans papier ni crayon. On peut toujours
raisonner intuitivement et suivre son inspiration. Cependant, la méthode de
résolution par système d'équations est un outil efficace et systématique.
Résolution
Notez
le systématisme de la présentation propice à la vision de la solution.
|
D'après
Télé Star Jeux de décembre 2014
|
Exemples 2 à 5 |
|
|
|
|
Couronne
(c), Anneau (a), diamant Bleu (b) et diamant Rouge (r)

Source: The Crown Puzzle
Voir Énigmes qui affolent le Net
![]()
|
|
|
|
Les trois équations de départ sont en jaune. On montre la "mécanique" et non pas les
valeurs.
Principe 1 - Avec les
équations 1 et 2 formez l'équation 4 sans x. 2 - Avec les
équations 2 et 3 formez l'équation 5 sans x. 3 - Avec les
équations 4 et 5 formez l'équation 6 sans x ni y, soit seulement z. |
|
|
|
|||
|
|
{ |
5x +
7y – 7z 2x +
4y – 3z –4x + 5y + 4z |
= – 8 = 0 = 35 |
|
|
{ |
5x +
7y – 7z 2x +
4y – 3z |
= – 8 = 0 |
|
|
{ |
2
(5x + 7y – 7z) 5 (2x
+ 4y – 3z) |
= 2 (– 8) = 0 |
|
|
{ |
10x
+ 14y – 14z) 10x
+ 20y – 15z) |
= –16 = 0 |
|
|
|
– 6y + z 6y – z |
= –16 = 16 |
|
|
{ |
2x
+ 4y – 3z –4x + 5y + 4z |
= 0 = 35 |
|
|
{ |
2(2x + 4y – 3z) –4x + 5y + 4z |
= 0 = 35 |
|
|
{ |
4x
+ 8y – 6z –4x + 5y + 4z |
= 0 = 35 |
|
|
|
13y – 2z |
= 35 |
|
|
{ |
6y – z
13y – 2z |
= 16 = 35 |
|
|
{ |
2 (6y – z)
13y – 2z |
= 2 . 16 = 35 |
|
|
{ |
12y – 2z
13y – 2z |
= 32 = 35 |
|
|
|
– y y |
= – 3 = 3 |
|
|
|
6y – z
18 – z z |
= 16 = 16 = 2 |
|
|
|
5x + 7y – 7z 5x + 7.3 – 7.2 5x x |
= – 8 = – 8 = – 15 = – 3 |
|
|
{ |
5.(–3) + 7.3 – 7.2 2.(–3) + 4.3 – 3.2 –4.(–3) + 5.3 +4.2 |
= – 8 = 0 = 35 |
|
Autre exemple avec trois
équations |
|
|
|
Résoudre ce système de trois
équations à trois inconnues. |
2x + 3y +
z = –2 (1) 5x + 4y +
z = –5 (2) 8x +
y + 2z = –9 (3) |
|
|
Avec deux équations, je fais
disparaître une inconnue (z, par exemple). |
3x + y =
–3 (4) = (2) – (1) |
|
|
Il me faut une autre
équation en x, y mais sans le z. |
10x + 8y + 2z = –10 (5) = 2*(2) 8x
+ y
+ 2z = –9 (3) 2x + 7y = –1 (6) = (5) –(3) |
|
|
Nous avons désormais un
système de deux équations à deux inconnues. |
3x
+ y = –3 (4) 2x + 7y
= –1
(6) |
|
|
Je multiplie la première par
7 pour disposer de la même quantité de y dans les deux équations. |
21x + 7y = –21 (7) = 7 * (4) 2x
+ 7y = – 1 (6) 19x = –20 (8) x =
–20/19 |
|
|
Calcul de y avec une équation
en x et y, par exemple la (4). |
3x + y = –3 3*(–20/19) + y = –3
|
|
|
Calcul de z avec une des
équations initiale, par exemple la (1). |
2x + 3y +
z = –2 (1)
|
|
|
|
|
|
Simultaneous
equations are a set of equations containing multiple
variables This set is often
referred to as a system of equations. A
solution to a system of equations is a particular specification
of the values of all variables that simultaneously satisfies all of the
equations. |
|
Devinette: les cartes de toutes les couleurs
|
Des
cartes disposées sur la table:
Combien
de cartes sur la table? Un
raisonnement intuitif laisse penser qu'il y a autant de cartes de chaque
couleur. En reprenant l'un des énoncés, on calcule: 12/3 = 4. La
mise en équation est simple, et la résolution relativement aisée. Il s'agit
d'un système de quatre équations à quatre inconnues. |
|
|
Mise en équations
|
Résolution
|
Voir Jeux
et énigmes
Devinette / Personnes – Solution
|
Si
l'un de A va dans B, alors ils y seront deux fois plus nombreux. 2(A – 1) = B + 1 Si
l'une de B va dans A, alors ils seront à égalité. B – 1 = A + 1 Système
de deux équations. De la seconde on tire: B – 1 +
1 = A + 1 + 1 B = A + 2 En
remplaçant dans la première: 2(A – 1) = A
+ 2 + 1 2A – 2 = A + 3 2A – 2 +
2 – A = A + 3 + 2 – A
A = 5 Et
pour B:
B = A + 2 = 5 + 2 = 7 |
|
Arthur
achète un litre de lait et un litre d'eau pour 5 euros. Bernard
achète un litre d'eau et un litre de soda pour 7 euros. Camille
achète un litre de lait et un litre se soda pour 4 euros. Si
Danièle achète un litre de lait, un litre d'eau et un litre de soda, combien
va-t-elle payer? Solution On
remarque que la somme des d'achats d'Arthur, Bernard et Camille correspond au
double des achats que veut réaliser Danièle pour 5 + 7 + 4 = 16 euros. Danièle
déboursera la moitié: 8 euros. Bonus Avec
les indications de cette page, vous êtes aussi capables de trouver que: Eau
= 4 €/ l, Lait = 1 €/ l et Soda = 3 €/
l. |
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()