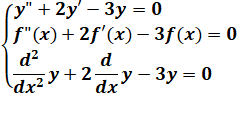|
Voir INDEX ÉQUATIONS >>>
|
On pose x la quantité de billes de Gérard. Gilbert en a x aussi; et a tous les deux cela fait x + x = 2x Avec celles de Daniel cela fait 2x + 5, ce qui donne le total de
billes dont on nous dit que c'est 25. On note l'égalité: 2x + 5 = 25 Retirons 5 billes de chaque côté (ce qui ne change pas l'équilibre de l'égalité): 2x = 20 La quantité de billes de Gérard, comme celle de Gilbert est donc 10 Vérifions: 2 x 10 + 5 = 25, c'est juste!
|
||
|
Définition |
|
|
|
Racines |
x2 – 11x + 30 5² – 11 x 5 + 30 = 0 6² – 11 x 6 + 30 = 0
x2 – 11x + 30 = (x – 5) (x – 6) |
![]()
|
Équation |
|
f(x) = g(x) |
|
Membres |
|
f(x) & g(x) |
|
Inconnue |
|
x |
|
Résoudre |
|
f(x) = g(x) |
|
Solution ou racine |
|
f(a) = g(a) |
|
Réduire |
|
|
|
Type |
|
x, y, z … |
|
|
P(x) = 0 L'équation du cercle
est une équation algébrique: x² + y² =
1. Elle définit un lieu géométrique qui est appelé une variété algébrique. |
|
|
Degré |
|
n dans axn + bxn-1
+… |
|
2e degré |
|
ax² + bx
+ c = 0 |
|
Système |
|
ax + by + c = 0 a'x + b'y +c' = 0 |
Voir Dicomot des Maths
![]()
|
|
||
|
Les équations algébriques étudiées au
collège puis au lycée ne sont que le commencement d'une longue liste
d'équations plus ou moins facile à résoudre. Les solutions sont des nombres
réels ou complexes. |
Équation algébrique ou
polynômiale du second degré ax² + bx
+ c = 0 Exemple x² + 3x + 2 = 0 (x + 2)(x + 1) = 0 x1 = et x2 = – 1
|
|
|
En fin de
lycée, on aborde les équations
différentielles et intégrales qui
au lieu de considérer une ou plusieurs inconnues, impliquent la variation
dans le temps ou dans l'espace de ces inconnues. Les solutions sont des fonctions
ou combinaison de fonctions. |
Équation
différentielle du deuxième ordre Exemple Trois écritures équivalentes
Solutions
Vérification avec c1 = 1 et c2 = 1 y = y' = exp(t) – 3 exp(-3x) y"= exp(t) + 9 exp(-3x)
|
|
|
Méthodes algébriques (comme exposé ci-dessus) La
résolution des équations différentielles n'est pas toujours évidente. Elles
n'ont pas toujours (même pas souvent) une solution analytique (sous forme de
fonctions). Méthodes topologiques Au
début du XXe siècle, on a commencé à utiliser des méthodes topologiques
(graphiques) pour obtenir au moins des informations qualitatives sur les solutions,
comme par exemple: sont-elles périodiques? Malheureusement encore bon nombre
d'équations différentielles échappent à cette méthode, par exemple celles qui
ont plusieurs périodes lesquelles peuvent être enchevêtrées de façon assez
complexe. Méthodes numériques avec ordinateurs Durant
les dernières décennies, les méthodes numériques se sont développées avec
l'usage des ordinateurs. Cependant,
ce n'est pas encore suffisant pour toutes ces équations sensibles à la
moindre variation des conditions initiales. Sans compter sur le cumul
exponentiel des erreurs d'approximation. Même en augmentant la capacité des
ordinateurs certaines équations résisteront toujours à donner une solution. Méthodes ergodiques Alors,
les mathématiciens ont recours à une méthode basée sur les probabilités, faisant partie de la théorie
de la mesure, dite théorie ergodique. Elle
transpose un problème de dynamique (souvent temporel) en examen de
probabilités à un instant donné. En gros, et c'est une image, elle repose sur
le fait que la croissance d'un arbre dans la forêt au cours des années serait
observable en regardant simplement l'ensemble de ses congénères à un instant
donné. |
||
Voir Divers
types d'équations différentielles en physique
|
Autres |
|
Pour les noms sans lien, se reporter aux ouvrages spécialisés (hors du champ de ce site) |
![]()
|
Origine |
|
|
Anglais |
Mathematical statement that two expressions
are equal. |
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Vocabula/GlosE/Equation.htm |
![]()