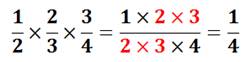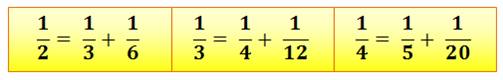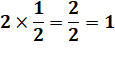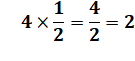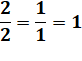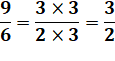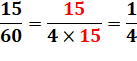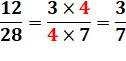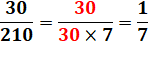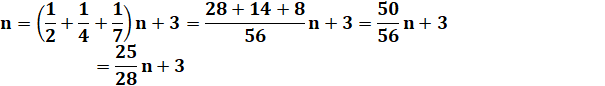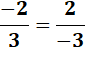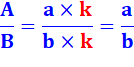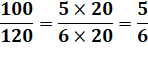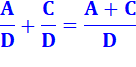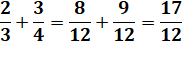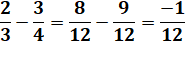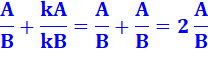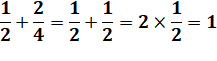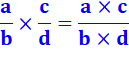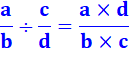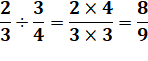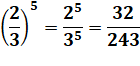|
||||||||||||||||||||||||||||||||||||||||||||||||
![]()
Humour
|
M'dam, pour bien vous montrer que j'ai
compris les fractions, je n'ai fait que la moitié de mon devoir (To show you
how well I understand fractions, I only did half of my homework). |
|
Apprentissage des fractions:
ta maman a deux pêches. Elle coupe la première en deux et la seconde en huit.
Que choisis-tu: un morceau de la première ou quatre morceaux de la seconde? -
Un morceau de la première, monsieur. – Voyons, tu n'as bien compris le cours:
un demi et quatre huitièmes c'est la même
chose. – Pas vraiment, parce qu'en coupant en huit, qu'est-ce que vous perdez
comme bon jus. Variante Le prof de math à son fils: - si tu as à
choisir entre une moitié d'orange ou huit seizièmes d'orange que choisirais-tu ? – La
moitié, bien sûr. – Portant, tu sais bien
que moitié et huit
seizièmes c'est la même chose. – Oui, mais je prendrai tout de même la
moitié. – Ça alors, mais pourquoi ? – Pour ne perdre le bon jus ! |
Voir Fractions de l'ivrogne / Pensées & humour
![]()
|
De mon expérience, même bons en calcul, les
enfants qui n'ont pas compris les fractions sont perturbés par la présence de deux nombres
(en haut et en bas). Une idée: insister pour dire que le nombre du bas
est comme une unité (comme des mètres ou
des kilogrammes). Conséquences: on prend soin de ne calculer qu'avec des
objets de même unités: 1 fois "un demi" + 1 fois "un
demi" = 2 fois "un demi". 1 fois "un demi" + 1 fois "un
tiers" = pas possible en l'état. Dans ce dernier cas, il faudra trouver un autre
moyen, une sorte de conversion d'unités qui sera appelée "réduction au même dénominateur" |
Voir Calcul avec
les briques de construction
Voir aussi: calcul des factions
avec l'analogie de la bête à pattes.
Diaporama réalisé par un enfant de 9 ans,
réfractaire aux fractions
![]()
|
FRACTIONS Introduction pour débutants Inévitable
tarte à partager … Une fraction de tarte, c'est une part de tarte ou
plusieurs parts de tartes, la tarte étant partagée (fractionnée) en deux,
trois, quatre, huit ou autres. Voir comment on
a réinventé les parts de tartes avec les briques du jeu de construction de
type LegoTM.
Diverses manières de présenter cette fraction 3/2 (trois
demis)
|
Voir Fractions
en diaporama, niveau collèges (métaphore de la bête à pattes)
Cours de 5e / Évaluation
de CM1 / Fractions
et méthode Singapour
Réponse à une question de primaire (10 ans) pour se lancer
|
Question:
Combien ça fait un quart
de 80? Réponse: Imagine que tu as 80 cartes dans ta main
et que tu veux les donner à tes quatre
copains et copines, mais il faut autant de cartes pour chacune. Alors comment
faire? Tu
donnes d'abord 10 cartes à chacun. Il te reste encore des cartes. Alors tu en
donnes encore 10. Tu as donné les 80 cartes et chacun en a 10 + 10 = 20.
Tu
constates que chaque enfant a reçu 10 + 10 = 20 cartes. Donc
80 divisé par 4 = 20. Normal car 4 x
20 = 80. Les
enfants sont 4. Alors, chaque enfant à
reçu un quart des 80 cartes. On écrit:
|
|
|
||
|
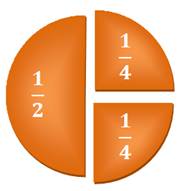
Moi et ma sœur avons décidé d'être sages; nous gardons la moitié de la tarte pour demain et nous partageons à
parts égales la deuxième moitié. Aujourd'hui, nous nous régalons avec un quart de tarte chacun.
|
|
|
Voir Partage de la tarte en parts égales
|
|
|
|
Une demi-heure, c'est 30 minutes. Car, une heure de 60
minutes divisée en deux, cela donne bien 30 minutes. Un quart d'heure, c'est une heure coupée en quatre;
soit 60 / 4 = 15 minutes. |
|
Récréation
|
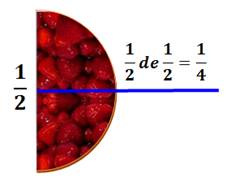
Que
vaut la moitié de la moitié? C'est
une moitié de tarte qui est encore coupée en deux parts égales. Ce qui donne
un quart de tarte. La
moitié du tiers, c'est un sixième. Le
tiers du tiers, c'est un neuvième. Les
deux tiers du tiers, c'est deux neuvièmes. Calculez
la moitié de deux tiers de trois quarts. Réponse à droite et illustration
ci-dessous. |
|
|
Pour
ceux qui préfèrent la représentation en barres
|
|
Voir Fractions
et méthode Singapour
|
|
||||
|
|
||||
|
|
|
|
|
|
|
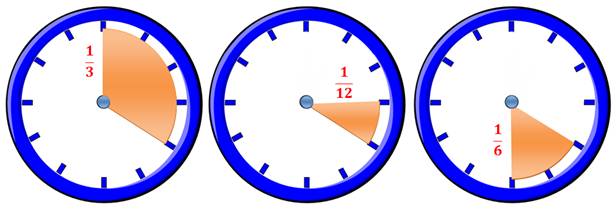
On
n'utilise pas beaucoup le tiers d'heure dans
le langage courant; on parle de 20 minutes; en effet, 60 / 3 = 20. On ne dit
jamais un douzième d'heure, mais 5 minutes (60
/ 12 = 5). Par contre, cette visualisation à travers l'horloge est commode
pour visualiser quelques fractions et les relations entre-elles. |
||||
![]() Attention
Attention
|
Ne
pas confondre la fraction 1/3
(un tiers de tarte) avec le nombre décimal
0,3 qui, lui,
représente la fraction 3/10. Dans le système décimal, les nombres
avant la virgule sont plus forts de 10 en 10; alors que, derrière la virgule,
ils sont moins forts de 1/10 en 1/10. Ainsi 0,3 peut également se lire: trois
dixièmes. 0,03 sera trois centièmes. |
Voir Nombres décimaux
Notation
|
La
notation
Cette
notation exprime d'abord la quantité d'entiers suivie d'une fraction dont la
valeur est inférieure à 1. Par exemple:
On
retrouve bien l'entier 7 suivi de la fraction 3/5 qui vaut 0,6 en notation
décimale. |
|
|
||
|
|
||
|
Pour passer d'une fraction à la suivante, il faut simplement ajouter
1/6 ou 1/12. |
|
|
|
Illustration des "distances" entre fractions. |
|
|
Suite Comparaison
avec fractions égyptiennes / Représentation
de la fraction 3/10 sur l'horloge
|
Il est toujours possible de transformer une fraction
unitaire (1/n) en somme de deux fractions dont les dénominateurs sont n+1 et
n(n+1). Par exemple:
Dit autrement: l'écart entre
une fraction (1/n) et la suivante (1/(n+1)) est égal à la fraction dont le
dénominateur est égal au produit des deux dénominateurs.
|
Suite
en Fractions égyptiennes / Partition et inverses / Série
en 1/(2x3)
|
|
||
|
|
Soit
à calculer:
Sur le dessin
ci−dessus, nous lisons la réponse: 1/12. Calcul: On divise tout en douzièmes de manière à ne calculer qu'avec les mêmes
parts de 1/12.
C'est comme si nous avions des objets de même unité: le douzième de
part. Il suffit de compter ces douzièmes: soit 4 auxquelles je retranche 3; il reste 1. Ou, en posant l'opération complète:
Avez-vous
remarqué que les nouveaux numérateurs (4 et 3) sont égaux aux anciens dénominateurs inversés (3 et 4) ? |
|
Mnémotechnique: en bas c'est le
type de fraction, son nom, sa dénomination;
en haut c'est le nombre de parts, son numéro.
Oups! Doucement! Plus d'explications sur le passage au même dénominateur
|
Une fraction ne change pas de valeur si on multiplie son
numérateur et son dénominateur par le même nombre.
|
Réduction au même dénominateur (fractions de même type). On pourrait
utiliser les portions de 1/12. Mais avec 1/6 c'est suffisant. En effet:
Ce faisant, les trois fractions sont en sixièmes de tarte. Nous pouvons
procéder au calcul de la somme de ces portions de 1/6:
|
|
Une
fraction ne change pas de valeur si on divise son numérateur et son dénominateur par le même nombre (sauf par 0).
Une
somme au numérateur peut être dédoublée en deux fractions de même
dénominateur. Exemple ci-contre avec 23/12. |
|
Remarques
|
Choix
du dénominateur-résultat: c'est le produit de tous les dénominateurs. Mais,
il est possible de simplifier le calcul par la connaissance du plus petit
commun multiple (PPCM) des dénominateurs élémentaires.
|
Voir Calcul
d'une expression avec des fractions (métaphore de la bête à pattes)
– Diaporama pour comprendre une fois pour toute!
|
|
||
|
|
|
|
|
|
|
|
|
|
Ainsi les fractions 9/6 et 3/2 sont égales. |
|
|
|
|
|
Voir Fractions versus méthode de
la fausse position
|
Exemples avec simplifications à ne jamais
faire, mais qui, ici, marchent …
|
Explication
|
|
Un motif répété en numérateur, un autre motif répété autant de fois au
dénominateur et la fraction est égale à la division des motifs. |
|
Voir Fractions
illicites / Décomposition des
nombres / Pannumériques
en fractions
|
Trouvez
un nombre tel que sa moitié plus son quart plus son septième plus 3 redonne
ce nombre.
Problème
qui nous vient de l'Antiquité (École de Pythagore). Nous
aurions pu tout aussi bien prendre une autre suite de fractions s'approchant
de 1 par défaut.
Notez que la première et la dernière
donne 19/20; normal: 1/3+1/6 = 1/2. |
Merci à
Guillaume Mahouin pour son "œil exercé"
|
|
||
|
Trouvez
la valeur de "FRACTION". Chacune des neuf lettres représente un
chiffre différent (cryptarithme). Ce
mot forme un nombre, de même que tous les groupes de lettres, comme TA. Tous
les chiffres sont
utilisés sauf le 0. |
FRACTIONS Les lettres sont telles que:
|
|
|
Première
observation On sait que:
|
F x F = F² = R => 2²
= 4 ou 3² = 9 Ce sont les seules possibilités d'obtenir un carré inférieur à
10. F = {2 ou 3} et R = {4 ou 9} |
|
|
Égalité
suivante |
F x R = A 2 x 4 = 8 oui 2 x 9 = 18 non (doit
être inférieur à 10) 3 x 4 = 12 non 3 x 9 = 27 non F = 2; R = 4 et A = 8 |
|
|
Suivante,
sachant
que les chiffres qui restent disponibles sont: {1, 3, 5, 6, 7 et 9}. |
F x O = C 2 x 1 = 2 non 2 x 3 = 6 oui 2 x 5 = 10 non etc. O = 3 et C = 6 |
|
|
Reste
à placer: {1, 5, 7 et 9}. Inspection
de la fraction TA / N. |
F = TA / N 2 = T8 / N 2 = 18 / 9 T = 1 et N = 9 |
|
|
Fraction
en TR avec {5 et 7}. |
F = TR / S 2 = 14 / S S = 7 |
|
|
Dernière
fraction avec {5}. |
2 = IF / FC I = 5 |
|
|
La
solution est unique. |
FRACTIONS = 248615397 |
|
Voir Pannumérique (nombres avec tous les
chiffres une seule fois)
Pour le plaisir
|
Question Existe-il une
fraction dont le numérateur est inférieur à son dénominateur qui serait égale
à une fraction dont le numérateur serait plus grand que son dénominateur? Exemple
|
![]()
Le coin
académique
|
|
|||
|
On peut multiplier ou diviser en haut et en bas par le même nombre On ne peut pas ajouter ou soustraire en haut et en bas par le même
nombre |
|||
|
Simplification Voir PGCD |
|
|
|
|
Même
dénominateur (MD) |
|
|
|
|
Addition et soustraction nécessitent la mise au même dénominateur |
|||
|
Addition (Après MD) |
|
|
|
|
Soustraction (Après MD) |
|
|
|
|
Addition
de fractions égales |
|
|
|
|
Les multiplications sont finalement très simples |
|||
|
Multiplication |
|
|
|
|
Division |
|
|
|
|
Puissance |
|
|
|
Toujours
simplifier les fractions lorsque cela est possible
Attention: ne jamais diviser par zéro!
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
DicoNombre |
|
|
Site |
|
|
Sites |
Vidéos pour apprendre les fractions avec
des Legos: quelques exemples de sites; il en existe beaucoup d'autres.
|
|
Cette page |
![]()