NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 27/03/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	OPTIQUE
Débutants Général	BASES			Glossaire Optique
INDEX Physique	Loi Snell-Descartes	Dioptres multiples	Lentilles	Horizon
		Sommaire de cette page >>> Distance a l'horizon >>> Et avec une paire de jumelles? >>> Calcul >>> Effet de la réfraction >>> Cagnes – Corse >>> Visibilité de l'ile d'Yeu

LIGNE d'HORIZON

Calcul de distances.

Cas de la Corse. Cas de l'île d'Yeu.

La fille qui rêvait d'horizon – Une enquête de l'inspecteur Canardo – Sokal – casterman – 1999

DISTANCE A L'HORIZON
Pour une personne dont les yeux sont de 1,73 mètre au-dessus du bord de la mer, l'horizon se trouve à environ 4 700 m ou 4,7 km.	Yeux de l'observateur; hauteur par rapport au niveau de la mer en mètres 1 1,73 5 10 20 50 100 500 1 000 10 000	Distance à l'horizon (km) 3,5 4,7 8 11 16 25 35 79 112 355

ET AVEC UNE PAIRE DE JUMELLES?
Question Est-ce que l'utilisation de jumelles change quelque chose ?	Réponse Non, cela ne change rien. Paradoxe? Non, car il faut considérer les objets posés sur l'eau. Du fait de la courbure terrestre, il n'est pas possible de voir derrière l'horizon.
Illustration Le globe terrestre est en bleu. La flèche rouge, c'est moi. Je peux voir le point vert, mais pas le point rouge et la limite (point orange) c'est tout simplement ce que nous appelons l'horizon. Une paire de jumelle ni change rien, même à fort grossissement ! En effet, il faut se souvenir que la lumière se propage en ligne droite. Quoique pas toujours… C'est le phénomène des mirages. Du fait d'une certaine humidité de l'atmosphère, la lumière se courbe. Alors, le point rouge peut devenir visible. C'est comme cela que, depuis Nice, en hiver, il est possible de voir la Corse. Il faut se lever tôt. On voit la Corse en l'air (oui, je dis bien) qui progressivement descend pour finalement disparaître en reprenant sa place invisible derrière l'horizon. Note Habitant dans les Alpes-Maritimes, j'ai la chance d'avoir observé ce phénomène des dizaines de fois. Ce phénomène est parfois relaté et photographié dans les journaux locaux.

CALCULS pour une personne au niveau de la mer
Littéral h taille de la personne a distance à l'horizon R² + a² = (R + h)² R² + a² = R² + 2Rh + h² a² = 2 Rh + h² En fait: h << R, on néglige h² a² = 2 Rh Numérique h = 1,73 m R = 6,378 10^6 m a² = 2 x 6,378 x 1,73 10^6 a² = 22,068 10^6 a = 4, 6976 4,7 km La formule en racine de 13 h donne: 4,742 km	a en km et h en m Voir Effet de la réfraction

Graphe: personne sur la plage Le graphe montre trois courbes: au milieu, avec la formule indiquée ci-dessus, et de chaque côté, les courbes exactes (avec a² = 2 Rh + h²) et les rayons min et max de la Terre (6 352 800 et 6 378 137 en m). La sensibilité au rayon terrestre est faible. L'écart est bien inférieur aux incertitudes de mesures dues au relief et aux vagues.	Comparaisons des formules de calcul
Graphes ci dessous On peut retenir que : les yeux à 2 m de hauteur par rapport au niveau de la mer, l'horizon dépasse les 5 km, et avec les yeux à 8 mètres, l'horizon se trouve à 10 km. Note: avec ces représentations, les trois courbes sont superposées donc confondues.

Distance de l'horizon (m) pour les personnes de 1 à 2,1 m ayant les pieds au niveau de la mer

Distance de l'horizon (m) pour des yeux de 0 à 10 m au-dessus du niveau de la mer

Effet de la réfraction

Dans la réalité, le calcul géométrique indiqué doit être corrigé en tenant compte de la réfraction des ondes électromagnétiques. La courbure des rayons provoque une sorte de soulèvement de l'horizon, éloignant sensiblement sa limite:

En navigation a vue (rayon lumineux): ajoutez 8,8 %

En réception radar (ondes à grande fréquence): ajoutez 14%.

Tableau indiquant la valeur du coefficient k selon le mode et les unités.

Selon la nature de l'atmosphère, le phénomène de réfraction peut être amplifié au point de produire le phénomène de mirage. Comme si la Terre était moins ronde.

Grand merci à Jéro Nimo

Cagnes-sur-Mer & Corse
Photo publiée par Nice-Matin le 23/10/2014 Voir Références pour de nombreuses photos de ce superbe phénomène que j'ai observé moi-même à de multiples reprises.
Sur la colline de Cagnes, mon œil se trouve à 50 m d'altitude. Quel est la hauteur c d'un sommet qui serait situé à Calvi pour qu'il soit visible depuis Cagnes? Nous disposions de trois équations. a² = 2Rh = 2 x 6,378 x 50 x 10^6 a = 25,25 km b = 180 – 25,3 = 154,74 c = 154,74² / (2 x 6,378 10^3) c = 1,877 km = 1 877 m Or le Mont Cinto culmine à 2 710 m. Il est visible en vision directe.	a + b = 180 km (Cagnes-Calvi) a² = 2Rh b² = 2Rc
Le Mont Cinto (altitude: c = 2 710 m) est situé à 205 km de Cagnes-sur-mer. À quelle altitude h doit être mon œil pour voir le sommet en vision directe? b² = 2 x 6 378 x 2,71 b = 185,926 km a = 205 – 185,9 = 19,1 km h = 19,1² / (2 x 6 378) h = 28,52 m Dès 30 mètres d'altitude le Mont Cinto est visible depuis la Côte d'Azur. Un petit coup de pouce de la réfraction permet de relever un peu la Corse et de voir un large panorama de celle-ci.	a + b = 205 km a² = 2Rh b² = 2Rc Même si le point du Mont Cinto est visible depuis les corniches de Nice, Saint-Laurent du Var ou de Cagnes, le phénomène mirage de janvier, février rend visible une plus grande partie de cette pointe Corse du Nord.

Ile d'YEU
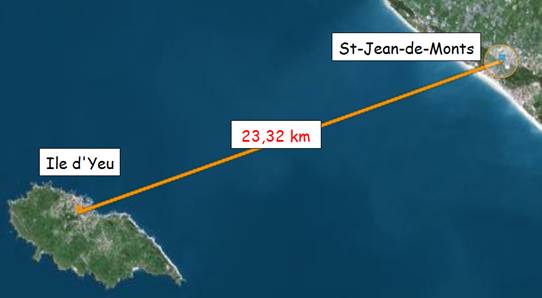
Ile visible depuis St-Jean-de-Monts? Angle apparent de l'ile: 24° (angle de vision horizontal). Superficie de 23,32 km² (palindrome!). Culminant à 32 m.
Ces images sont extraites du Géoportail IGN
Calcul de visibilité directe L'abaque suivant est universel. Les trois courbes correspondent à trois positions des yeux: 2 m, 10m ou 20m; Les ordonnées donnent la distance en kilomètre de l'objet observé; et Les abscisses déterminent jusqu'à quelle altitude en mètres l'objet reste caché Lecture un observateur situé à St-Jean-de-Monts regardant en direction de l'Ile d'Yeu (traits bleus) 1) Pour un observateur au niveau de la mer (yeux à 2m), toute la partie en dessous de 20 m n'est pas visible. Le profil situé au-dessus de 20 à 25 m devrait émerger. 2) En se hissant à 10 à 15 m, la partie de l'ile au-dessus de 10 m d'altitude devrait devenir visible. 3) Sur le rivage, à 20 ou 25 m de haut, pratiquement toute l'ile devient visible Ne connaissant pas du tout cet endroit, je prends des précautions en donnant des fourchettes de calcul. Si vous avez l'expérience locale, je serais heureux de partager vos observations. Tous ces calculs devraient également être revus et corrigés en tenant compte de la réfraction ordinaire de la lumière. Témoignage La théorie du mirage me semblait plutôt viable puisque ici les habitants ont l'habitude de dire que lorsque l'on voit bien l'île d'Yeu c'est signe de mauvais temps. Des conditions météorologiques (humidité et air plus froid) qui peuvent provoquer un mirage, je crois. Paul B.

Suite	Terre Distance entre points géographiques Sonars
Voir	Niveau de la mer Optique – Glossaire et index Théorème de Pythagore Rayon de la Terre Trait de côté – Longueur? France
Diconombre	Nombre 4700
Article	Vers l'horizon et au-delà – Jean-Michel Courty et Édouard Kierlik Pour la Science n° 502, pages 88 à 90 – Août 2019 – Réfraction sur le lac du Bourget
Sites	La Corse vue du Continent – Photos et liens Voit-on réellement la Corse? – Explications et Photos Ray and Shadows – Phénomènes optiques Peut-on voir la Corse de menton? – Explications La Corse vue de la Côte d'Azur – YouTube
Sites	Calcul de la distance à l'horizon – astronoo.com Horizon (physique) – Wikipédia Horizon – Wikipedia (anglais) – pour les unités anglaises et d'autres formules Horizon cosmologique – Wikipédia
Cette page	http://villemin.gerard.free.fr/aScience/Physique/OPTIQUE/Horizon.htm