NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 28/04/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	JEUX
Débutants Énigmes	CARTES				Glossaire Combinatoire
INDEX Cartes Jeux Dénombrement	Cartes (hasard)	Réussite	Fractale	Poker
	Carrés magiques	Deux par deux	Château de cartes
		Sommaire de cette page >>> Jeu de cartes aléatoire >>> Deux cartes noires

HASARD & CARTES

L'exemple donné ci-dessous illustre le cas d'emploi:

de la multiplication des probabilités (événement dépendants)

ou de l'addition des probabilités (événement exclusifs)

Voir Principes additif et multiplicatif

Jeu de cartes aléatoire
Mélanger les cartes 6 fois suffit pour disposer des cartes réparties aléatoirement. Le mélange américain (riffle shuffle) est le plus efficace: couper le paquet en deux et regrouper les deux paquets en intercalant leurs cartes respectives. Il y a une transition abrupte entre 6 et 8 mélanges: moins de 6 et c'est mal mélangé, plus de 8 et c'est parfait. Ce phénomène a été mis en évidence dans de nombreux processus aléatoires. L'état d’équilibre est atteint non pas progressivement, mais de manière abrupte. Avec une mélange par coupes successives à la française, il faudrait 10 000 opérations pour atteindre la perfection. En prenant la carte du dessus et en l'insérant n'importe où dans le paquet, 205 opérations sont nécessaires. Le calcul statistiques donne: n log n = 205, 46 … en moyenne. Un calcul plus intuitif donne (Voir ref. Hohman): Note: Il y a 52 ! = 8,06 x 10^67 jeux possibles. Una quantité astronomique telle que, lors d'un mélange, il est presque sûr que votre jeu soit le premier de tout les temps, disposé de la sorte. En effet, l'Univers existe depuis "seulement" 4,32 x 10^17 secondes.	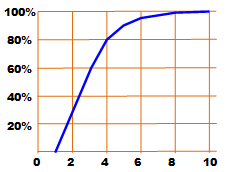Mélange américain Efficacité de ce mélange Mélange français

Voir Nombre 6

DEUX CARTES NOIRES
Problème On a 10 cartes: 6 cartes noires, et 4 cartes rouges. Posées sur la table, vues de dos: On en tire 2. Quelle la probabilité d'en tirer 2 noires ?

Solution 1
On tire une carte. On a 6 chances sur 10 d'en tirer une noire.	PUNE NOIRE	= 6 / 10
Il reste 9 cartes dont 5 noires et 4 rouges. On a 5 chances sur 9 d'en tirer une noire.	P AUTRE NOIRE	= 5 / 9
On note que le tirage de la 2^e carte dépend du tirage de la première.	Les tirages sont dépendants
Dans ce cas la probabilité pour que les 2 cartes soient noires est le produit des deux.	P 2 NOIRES	= 6 / 10 x 5 / 9 = 30 / 90 = 1/ 3

Solution 2
On calcule la probabilité de ne pas avoir deux noires. C'est le cas lorsqu'on tire: une noire et une rouge, une rouge et une noire, une rouge et une rouge.	PPAS 2 N	= P1N+1R + P1R+1N + P1R+1R
Analyse des trois cas
Probabilité de tirer une noire et une rouge.	P1N+1R	= 6/10 x 4/9 = 24 / 90
Probabilité de tirer une rouge et une noire.	P1R+1N	= 4/10 x 6/9 = 24 / 90
Probabilité de tirer une rouge et une rouge.	P1R+1R	= 4/10 x 3/9 = 12 / 90
On note que les trois cas sont incompatibles.	Les tirages sont incompatibles on dit aussi exclusifs
Bilan
Dans ce cas, la probabilité des trois cas est égale à la somme des probabilités. C'est la probabilité de ne pas tirer deux noires.	PPAS 2 N	= (24+ 24 + 12) / 90 = 60 / 9 0 = 2/3
Vérification
Tirer deux noires ou ne pas tirer deux noires est une certitude. Sa probabilité est égale à 1. Ce que l'on vérifie.	1	= P 2 N + P PAS 2 N = 1/3 + 2 /3

Suite	Réussite Voir haut de page Cartes – Index
Voir	Chances aux tirages Combinatoire - Développement Combinatoire - Glossaire Dénombrement Dénombrement - Index Jeux – Index Jeux de hasard Logique – Index Paradoxes Probabilités - Glossaire Trois pièces
DicoNombre	32 cartes 54 cartes
Sites	Shuffling – Wikipedia The Math of Card Shuffling – Fred Homan The Best (and Worst) Ways to Shuffle Cards – Numberphile How many times should youshuffle a deck of cards?** – Brad Mann Card-Shuffling Analysis** – Dean Katsaros and Yaping Yuan The Mathematics of Card Shuffing** – JohanJonasson Shuffling cards and stopping times** – David Aldous & Persi Diaconis
Cette page	http://villemin.gerard.free.fr/Puzzle/HazCart.htm