NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 04/10/2024 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50

	Page 50 (980-999)		Page 51 (1000-1019)		Page 52 (1020-1039)		Page 53 (1040-1059)		Page 54 (1060-1079)
	Page 55 (1080-1099)		Page 56 (1100-1119)		Page 57 (1120-1139)		Page 58 (1140-1159)		Page 59 (1160-1179)

BRÈVES de MATHS – Page 50

Un millier de faits et chiffres

sur les nombres et les mathématiques

Curiosités et amusements mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

980. Carré et cercle
La question Comment retenir les formules de calcul du périmètre et de l'aire du cercle ? Le plus simple Je sais qu'il y a un 2 un Pi et un R, mais où est le 2 ? Ah oui ! Une aire est un produit de longueur, donc une longueur au carré. Je mets donc R². Ce qui donne: A = π R² et P = 2 πR. Sinon Je reconstruis cette figure mentalement. Le périmètre de ce carré et 8 R, celui du cercle est juste un peu plus petit avec environ 6 R; en fait 2 π R. L'aire de ce carré est 4R², celle du disque est juste inférieure. Environ 3R²; en fait π R².		Note: on se souvient que, par simplification, on écrit:
Brèves associées	>>> Cercle, carré et cordes		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Formulaire du cercle		>>> Cercle – Index

981. Chiffres de l'économie

Brèves associées	>>> GAFAM et trillion de dollars	>>> Brèves Économie – Index
Pour en savoir plus	>>> PIB France	>>> Économie – Index >>> GAFAM-A …

982. Produit dans le triangle de Pascal
Propriété Dans le triangle de Pascal, le produit des pétales bleus est toujours égal au produit des pétales jaunes. Exemple 6 × 35 × 28 = 7 × 15 × 56 = 5 880		Triangle de Pascal
Brèves associées	>>> Mot de Fibonacci et sa fractale		>>> Brèves Itérations – Index
Pour en savoir plus	>>> Triangle de Pascal		>>> Itérations – Index

983. Factorielle – Chiffres significatifs
Quantité de "0" La quantité de "0" est due aux facteurs 5 et 10.		5! = 120 avec un seul "0" car un seul 5 comme facteur. 10! = 3628800 avec deux "0" car 5 et 10 comme facteurs
Formulation Les crochets fermés en bas signifie plancher (en anglais: floor). Pour n = 50, il y a 12 zéros. Pour n = 100, il y a 24 zéros.			Exemple pour n = 50 pour lequelQ₀ = 12
Trouver les deux derniers chiffres significatifs d'une factorielle: dizaines (d) et unités (u). Mod 100 signifie: reste de la division par 100. Ajuster le mod 100 à la quantité désirée de chiffres.					Exemples Pour 50, N_du = 12 Pour 100, N_du = 64
Brèves associées	>>> Factorielles et files indiennes			>>> Brèves Compter – Index
Pour en savoir plus	>>> Factorielles – Chiffres significatifs			>>> Compter – Index >>> mod (modulo)

984. Nombres 123 et 321
		Divisions produisant des quotients avec deux décimales singulières: croissance de l'une et décroissance de l'autre.
Brèves associées	>>> Égalités surprenantes		>>> Brèves Magie – Index
Pour en savoir plus	>>> Pépites numériques		>>> Nombre 321

985. Nombres symétriques

Racine des nombres palindromes "en toit" (En référence à la symétrie par rapport au chiffre central) Note: la racine carrée de 123456789 est 11111,111060… Amusements sur calculette proposés par Paul Villemin Voir Brève de maths n° 583 / Palindromes	n		Exemple de multiplication posée
	121	11
	12321	111
	1234321	1 111
	123454321	11 111
	12345654321	111 111
	1234567654321	1 111 111
	123456787654321	11 111 111
	12345678987654321	111 111 111

Comparaison

Brèves associées

>>> Carrés et concaténation

>>> Brèves Formes – Index

Pour en savoir plus

>>> Racines carrées des repunit

>>> Repunits

986. Château de cartes
Problème Combien de cartes pour construire un château de cartes de n étages ? Commentaires Sur ce château de quatre étages (n = 4) chaque triangle est formé de trois cartes, sauf au pied. On compte les triangles
Liste des quantités de cartes pour un château de n rangées de 1 à 50: 2, 7, 15, 26, 40, 57, 77, 100, 126, 155₁₀, 187, 222, 260, 301, 345, 392, 442, 495, 551, 610₂₀, 672, 737, 805, 876, 950, 1027, 1107, 1190, 1276, 1365₃₀, 1457, 1552, 1650, 1751, 1855, 1962, 2072, 2185, 2301, 2420₄₀, 2542, 2667, 2795, 2926, 3060, 3197, 3337, 3480, 3626, 3775₅₀. Record de 1992 pour le château le plus haut par Bryan Berg: 75 étages. Au lieu des triangles, il arrange les cartes verticalement en carrés. Le record en 12 heures atteint 50 étages – Tian Rui en 2022.
Brèves associées	>>> Château et douves	>>> Brèves Jeux – Index
Pour en savoir plus	>>> Jeux de cartes	>>> Dénombrement >>> Jeux et énigmes – Index

Anglais House of cards, card tower, card castle

987. Triangle inscrit dans le cercle
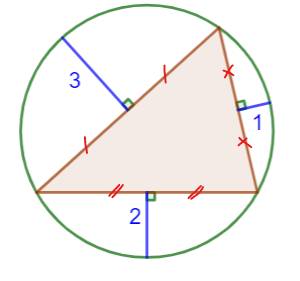
Problème On donne un cercle et un triangle inscrit. On connait la longueur des segments indiqués, portés par les médiatrices des côtés. Quelle est l'aire du triangle ? Longueur des côtés ? Indice Calculer les longueurs des côtés et l'aire en fonction du rayon du cercle, puis trouver la longueur de ce rayon. Commentaire La solution n'est pas aussi simple que ne le laisse supposer la figure !		Quelle est l'aire du triangle ? Pour info: cette figure est exacte en proportions.
Brèves associées	>>> Triangle et rectangle – Périmètre		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Solution de ce problème >>> Divers problèmes de géométrie		>>> Cercle >>> Triangle >>> Médiatrice

988. Combien de carrés ?
Question Comment compter tous les carrés présents dans une grille carrée ? Ne pas oublier les carrés de toute taille. Calcul Si n est la taille de la grille (quantité de carrés élémentaires sur un côté), alors la quantité totale de carrés est égale à la somme de tous les nombres au carrés de 1 à n.		Formules Exemple n = 4 Q(4) = 4² + 3² + 2² + 1² = (4 × 5 × 9)/6 = 30
Illustration Liste pour n de 1 à 25 1, 5, 14, 30, 55, 91, 140, 204, 285, 385, 506, 650, 819, 1015, 1240, 1496, 1785, 2109, 2470, 2870, 3311, 3795, 4324, 4900, 5525
Brèves associées	>>> Carrés dans le carré – Empilement		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Combien de carrés dans le carré		>>> Carrés dans une grille

989. Narcissiques généralisés
Type de partition des nombres Nombres égaux à la somme de ses chiffres à une puissance ou des chiffres d'une puissance chacun pouvant être également portés à la même puissance. Nombres dits: narcissiques de Keith. Description Le nombre 21, par exemple, est la somme de ses chiffres (2+1) et de ceux de son cube (9+2+6+1). C'est aussi la somme de ses chiffres (2+1) et de ceux de sa puissance cinquième (4+0+8+4+1+0+1). Autre exemple, le nombre 205 est la somme des chiffres de son carré (42 025), chacun porté au cube.		Exemples
Brèves associées	>>> Nombres narcissiques		>>> Brèves Types de nombres – Index
Pour en savoir plus	>>> Nombres narcissiques généralisés		>>> Table des nombres narcissiques

990. Principe des tiroirs
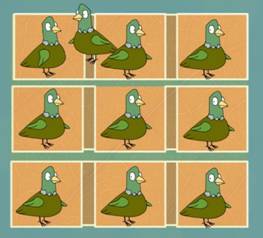
Principe des tiroirs. *Se dit pigeonhole principle* (principe du pigeonnier) en anglais Dans la situation de gauche, où se place le dixième pigeon ? Nécessairement dans l'un des neuf trous ! Un des trous contiendra au moins deux pigeons.**		Dans la situation de droite, le même principe s'applique même pour plus de pigeons. Si n est la quantité de trous: à gauche: n + 1 pigeons. à droite: 2n + 1 pigeons.

Brèves associées	>>> Sous-ensembles de [1, 2, 3, 4]		>>> Brèves Dénombrement – Index
Pour en savoir plus	>>> Principe des tiroirs		>>> Dénombrement – Index

991. Relation entre 99 et 199
Petite énigme Calcul simple avec une identité remarquable: développement du carré (a + b)² = a² + 2ab + b² n est la quantité de chiffres répétés
Brèves associées	>>> Multiplication par 111	>>> Brèves Calcul – Index
Pour en savoir plus	>>> Nombre 100	>>> Identités remarquables

992. Nombre 333 et 111 222
Curiosité qui produit un motif répétitif D'une manière générale:		Son calcul Avec d'autres chiffres
Brèves associées	>>> Nombre 100		>>> Brèves Nombres – Index
Pour en savoir plus	>>> Nombre 333		>>> DicoNombre

993. Trois cercles tangents
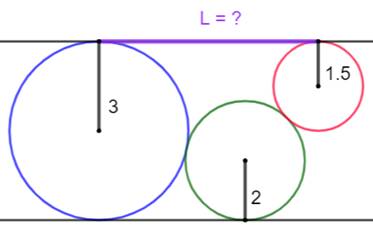
Problème Trois cercles tangents de diamètre 6, 4 et 3. Quelle est la valeur de L ?
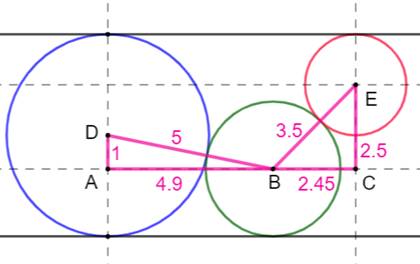
Solution Joindre les centres des cercles deux à deux pour faire apparaitre deux triangles rectangles ABD et BCE. Avec le théorème de Pythagore: AB² = DB – AD² = 5² – 1² = 24 = 4 × 6 BC² = BE² - CE² = (7/2)² – (5/2)² = 24/4 = 6
Brèves associées	>>> Cercles, intersections et régions	>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Trois cercles tangents	>>> Théorème de Pythagore

994. Multiplications par 9…9
Il suffit de faire -1 (bleu) et soustraire; le résultat (rouge) tombe directement.
Brèves associées	>>> Multiplication par 9 – Avec les doigts	>>> Brèves Opérations – Index
Pour en savoir plus	>>> Opérations avec 9 et 9…9	>>> Nombre 9

995. Démonstrations muettes

Brèves associées	>>> Calcul avec racines carrées	>>> Brèves Algèbre – Index
Pour en savoir plus	>>> Comparaison des moyennes	>>> Moyennes

996. Ramsey: R(3,3) = 6
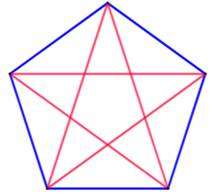
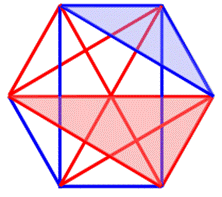
Cinq sommets Ce pentagone avec ses diagonales est colorié avec deux couleurs. Il serait toujours possible de dessiner un triangle rouge ou bleu. Mais, cet exemple montre qu'il est aussi possible d'éviter d'avoir un de ces triangles d'une seule couleur.		Six sommets Avec un hexagone et ses diagonales, toujours avec deux couleurs, le coloriage de tous les segments fera inévitablement apparaitre un triangle d'une seule couleur. Vous pouvez imaginer un jeu de coloriage tour à tour. Le premier qui a dessiné un triangle de sa couleur a perdu.
Conclusion: nombre de Ramsey Avec six sommets, et pas cinq, un triangle bleu ou rouge sera toujours présent. On dit que le nombre de Ramsey R(3, 3) est égal à 6, six comme la quantité de sommets de l'hexagone et trois symbolisant les triangles.		Application: théorème des amis Supposons que six personnes soient réunies lors d'un dîner. Alors, il y a nécessairement un groupe de trois personnes à la fête qui sont: soit toutes des connaissances communes, soit toutes des étrangers les uns pour les autres.
Brèves associées	>>> Paradoxe de Banach-Tarski		>>> Brèves Graphe – Index
Pour en savoir plus	>>> Nombres de Ramsey		>>> Moyennes

997. Triangle équilatéral inscrit
Construction Un cercle de rayon unité (r = 1). Construction classique de la rosace. On dispose de six points également repartis sur la circonférence. En choisissant un point sur deux, on construit le triangle équilatéral. But Calculer la longueur du côté du triangle équilatéral, son aire et le ratio entre les deux surfaces disque et triangle équilatéral. Aires		Pour un cercle unité, la longueur du côté du triangle équilatéral inscrit est racine de 3.
Brèves associées	>>> Triangle inscrit dans cercle – Énigme		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Cercles dans le triangle équilatéral		>>> Triangle équilatéral

998. Calcul avec des puissances
Comment calculer cette simple expression en puissance de 9 ? Ce n'est pas 9³⁰ ! C'est trois fois le nombre 9¹⁰. Et, en remarquant que 9 = 3², il est possible d'associer ce 3 avec les 3² sous la puissance.		Pour aller plus loin:
Brèves associées	>>> Multiplications originales		>>> Brèves Calculs – Index
Pour en savoir plus	>>> Calculs avec des puissances		>>> Puissances et exposants

999. Longueur – Énigme
Problème Sur cette figure, il y a trois rectangles dont on connait deux longueurs et deux aires. Calcul la longueur x. Solution * en notant que a/b = x/y ó ay = bx		Le calcul de l'aire des rectangles bleus en fonction de x permet de trouver la valeur de x.
Brèves associées	>>> Le compte est bon		>>> Brèves Calculs – Index
Pour en savoir plus	>>> Système d'équations		>>> Énigmes virales

Retour	Brèves de maths – Page 49
Suite	Brèves de maths – Page 51
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve50.htm

980. Carré et cercle

981. Chiffres de l'économie

982. Produit dans le triangle de Pascal

983. Factorielle – Chiffres significatifs

984. Nombres 123 et 321

985. Nombres symétriques

986. Château de cartes

987. Triangle inscrit dans le cercle

988. Combien de carrés ?

989. Narcissiques généralisés

990. Principe des tiroirs

991. Relation entre 99 et 199

992. Nombre 333 et 111 222

993. Trois cercles tangents

994. Multiplications par 9…9

995. Démonstrations muettes

996. Ramsey: R(3,3) = 6

997. Triangle équilatéral inscrit

998. Calcul avec des puissances

999. Longueur – Énigme