|
||||||||||||||||||||||||||||||||||||||||
![]()
|
POLYOMINOS Formes
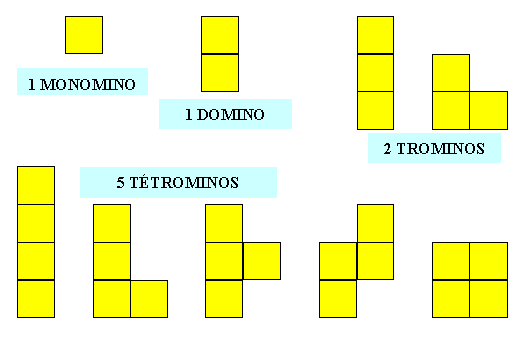
réalisées avec des carrés assemblés. Puzzle consistant à réaliser des figures, comme avec le Tangram. Aussi simple d'apparence. Des milliers de solutions. Et pourtant, ils ne se laissent pas faire! |
|
|
|
|
Définition
Exemples
Voir Pentominos
/ Tétris
et pavage |
|
|
|
|||||
|
On
les trouve dans le commerce. |
|||||
|
n |
Nom |
Pleins |
Creux |
Total = Pn |
|
|
2 |
1 |
|
1 |
||
|
3 |
Trominos |
2 |
|
2 |
|
|
4 |
Tétrominos Quadriminos |
5 |
|
5 |
|
|
5 |
12 |
|
12 |
||
|
6 |
35 |
|
35 |
||
|
7 |
Heptominos |
107 |
1 |
108 |
|
|
8 |
Octominos |
363 |
6 |
369 |
|
|
9 |
Nonominos Enneominos |
1 248 |
37 |
1 285 |
|
|
10 |
Dekominos |
4 460 |
195 |
4 655 |
|
|
11 |
|
|
|
17 073 |
|
|
12 |
|
|
|
63 600 |
|
|
13 |
|
|
|
238 591 |
|
|
14 |
|
|
|
901 971 |
|
|
15 |
Pentédécominos |
3 002 520 |
424 056 |
3 426 576 |
|
|
16 |
|
|
|
13 079255 |
|
|
17 |
|
|
|
50 107 909 |
|
|
18 |
|
|
|
192 622 052 |
|
|
19 |
|
|
|
742 624 232 |
|
|
20 |
|
|
|
2 870 671 950 |
|
Voir
Formation
des noms avec l'exemple des polygones
|
N-ominos creux |
|
|
|
|
|
Dénombrement |
|
|
(démontré par David
Klamer)
n3,72 < Pn < n4,65 |
|
|
|
|||
|
1907 |
Henry Dudeney |
|
|
|
1930 |
|
|
|
|
1935 |
|
|
|
|
1953 |
Salomon Golomb |
|
|
|
1958 |
|
|
|
|
1957 |
Martin Gardner |
|
|
|
1965 |
Salomon Golomb |
|
|
|
1996 |
George Martin |
|
|
|
|
||
|
Domino |
|
|
|
Triminos droits |
|
|
|
Triminos équerre |
|
|
|
Tétraminos |
|
|
|
|
||
Voir Échecs / Carrés parfaits
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Site |
![]()